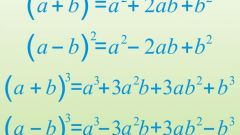You will need
- Scientific calculator
Instruction
1
In the calculator, typically there is a function to calculate the natural logarithm, i.e. the logarithm of any number to base e. But from the properties of the logarithm and the rules of operations on them, you can calculate a logarithm on the calculator on any other basis. For this you need to apply the formula of transition from the basis e to the desired new base.
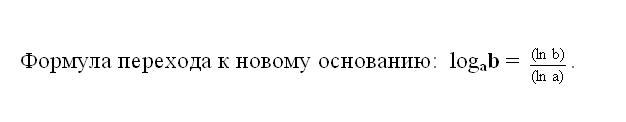
2
Taking into account the transition formula, perform the calculation of the logarithm of the number b for the base and on the calculator, storing the generated intermediate results in the memory device. To do this, first calculate the natural logarithm of the number a, which is the basis of your original logarithm. Click on the calculator press [MC] to clear the calculator memory. Then dial the number of the base and click on the function of the natural logarithm [ln].
3
Save the resulting value of the logarithm in memory using the button [M+]. Next, clean the window with the results for further calculations by pressing [C].
4
Calculate the natural logarithm of the number b defined in your source log. To do this, enter on the calculator sequence: first b, then [ln]. Get the logarithm of a given number, but on the basis of E.
5
Calculate the logarithm given base. To do this, divide the last, the value of the logarithm of b to the memory an intermediate value of the logarithm. Click: [/] and [MR]. On screen display the first calculated number. Perform division by pressing [=]. The calculator will give you the screen the value that is the logarithm of the given number a in base b.