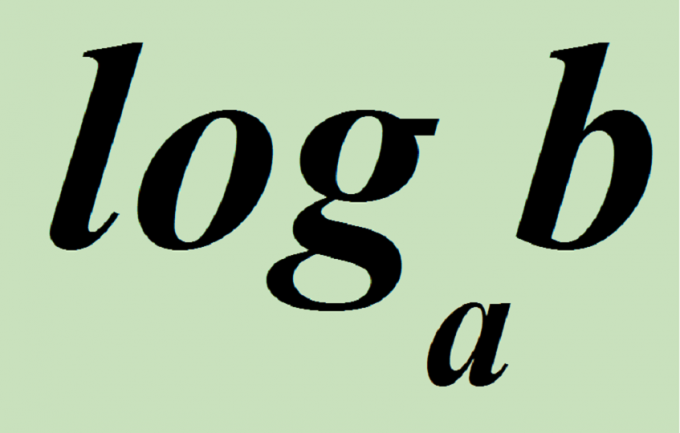Instruction
1
From the definition of the logarithm it follows that in order to solve the equation logaX=b must make the same transition a^b=x if a>0 and a is not equal to 1, i.e. 7=logX base 2, then x=2^5, x=32.
2
When solving logarithmic equations often go to neravnomernoi transition, so the need to verify the roots by substituting in the given equation. For example, given the equation log(5+2x) base-0,8=1, by neravnomernoi transition, it turns out log(5+2x) base 0,8=log0,8 on the basis of 0.8, it is possible to omit the sign of the logarithm, then the equation 5+2=0,8, solving this equation we get x=of-2.1. When you check x=of-2.1 5+2x>0, which corresponds to the properties of the logarithmic function (the domain of the logarithmic region is positive) therefore x=of-2.1 - root equation.
3
If the unknown is at the base of the logarithm, then this equation is solved in the same ways. For example, this equation, log9 on the ground (x-2)=2. Acting as in the previous examples, we get (x-2)^2=9, x^2-4x+4=9, x^2-4x-5=0, solving this equation is X1=-1, X2=5. Since the basis functions must be greater than 0 and not equal to 1, it remains the only root of X2=5.
4
Often when solving logarithmic equations you must apply the properties of logarithms:
1) logaXY=loda[X]+loda[Y]
logbX/Y=loda[X] loda[Y]
2) logfX^2n=2nloga[X] (2n is even)
logfX^(2n+1)=(2n+1)logaX (2n+1 - odd number)
3) logX with base a^2n=(1/2n)log[a]X
logX with base a^(2n+1)=(1/2n+1)logaX
4) logaB=1/logbA, b not equal 1
5) logaB=logcB/logcA, c is not equal to 1
6) a^logaX=X, X>0
7) a^logbC=clogbA
Using these properties, you can reduce the logarithmic equation to a simpler type, and then already to solve the above-mentioned ways.