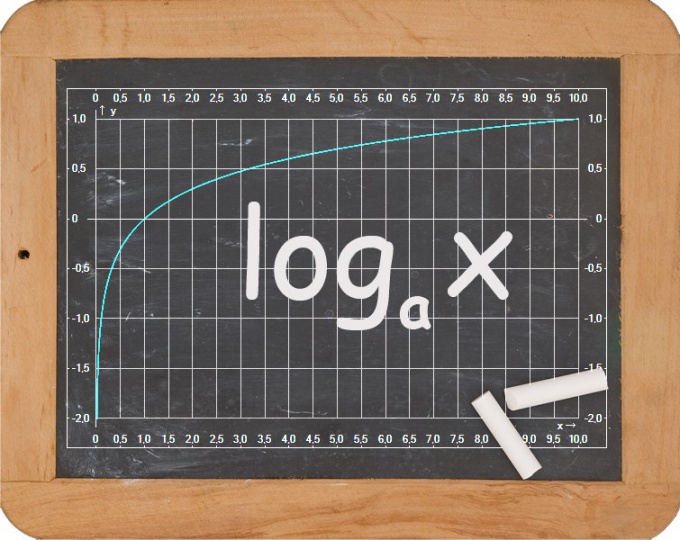Instruction
1
By itself, finding the logarithm from the logarithm of any special change does not imply - just follow sequentially those two operations. The only feature to begin with inside the logarithm, i.e., which is podogrevom expression of the other. For example, if you want to find log₃ log₂ 512, start with the calculation of the logarithm of 512 base 2 (log₂ 512 = 9), and then calculate the logarithm of the obtained result with the base 3 (log₃ 9 = 2), i.e. log₂ log₃ 512 = log₃ 9 = 2.
2
If one of podlovkina expression is a polynomial, use the transformation equations before proceeding to the calculations. For example, the sum of the logarithms on the same basis transform in the logarithm of the works of their podlovkina expressions to the same cause: logₐ (logᵤ x + logᵤ y) = logₐ logᵤ (x*y). In a similar way transform and difference of logarithms: logₐ (logᵤ x - logᵤ y) = logₐ logᵤ (x/y).
3
In some cases, podogretoe if the expression contains a number or variable raised to a power, it becomes possible to simplify the expression. For example, used in the first step of example log₃ log₂ 512 can be represented in this form: log₃ log₂ 2⁹. This allows you to see 9 out of sign of internal of the logarithm and the need to calculate the logarithm of 512 will disappear, as log₃ log₂ 2⁹ = log₃ (9*log₂ 2) = log₃ (9*1) = 2.
4
Described in the previous step the rule can be applied to the logarithms of expressions containing the root or fraction. To do this, imagine the root in the form of a fractional exponent. For example, if you need to find log₃ log₂ ⁹ √2, ⁹ √2 can be represented as 2 to the power of 1/9. Then log2 ⁹ √2 = 1/9 * log₂ 2 = 1/9 = 1/32 = 3-2. And log₃ 3-2 = -2. All these transformations are allowed to do without calculations and to record the decision: log₃ log₂ ⁹ √2 = log₃ (1/9 * log₂ 2) = log₃ (1/9) = log₃ (1/32) = log₃ 3-2 = -2.