How to solve a function

If you want to find the value of the function, using the formula, substitute in this formula instead of the argument (x), its valid values, i.e. values that are included in its scope. For this you need to find a domain of valid values for this function.

To find the domain of the function, determine what type she has. If the function of the form y = a/b, its domain would be all values except zero. The number a is any number. To find the area of function definition, radical expressions, provided the even indicator, this expression must be greater than or equal to zero. Finding the domain of the function the same expression, but with an odd index, keep in mind that x can be any number in that case, if the radical expression is not a fraction. Finding the domain of logarithmic functions, use the rule that expression which stands under the sign of logarithm must be a positive value.

Finding the domain of the function, go to it. For example, to solve the function: y = 2.5 x – 10 when x = 100, substitute in this formula x is the number 100. This operation will be as follows: y = 2.5 x 100 – 10; y = 240. This number is the required value of the function.

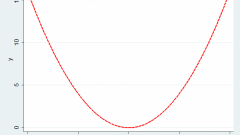
To find the value of the function using the graph, put in a rectangular coordinate system on the axis OX of the value of the argument (the point corresponding to the argument). Then, from the point of the guide perpendicular to the intersection of it with the plot function. From the resulting points of intersection of the perpendicular with the plot function, we drop a perpendicular on the axis OU. The base is constructed perpendicular will meet the desired value of the function.

If the function is set to table, then each argument value there is a corresponding value of the function.