You will need
- Protractor, ruler.
Instruction
1
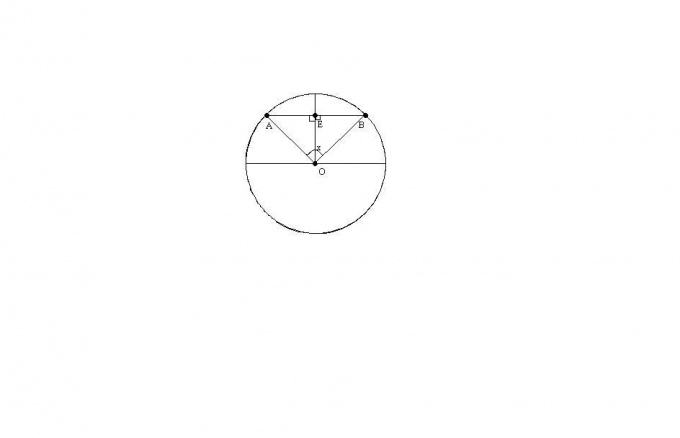
Let the known length of the chord AB and the angle AOB between the radiiconducted to the ends of the chord. We find these data the radius of the circle with center at point O.
2
Triangle AOB is isosceles because OA = OB = R. By a property of an isosceles triangle the height of the OE is a median and a bisector of the angle AOB. Denote the angle AOB for x
Triangle AEO is rectangular with right angle AEO. Since the height TH is also the bisector of the angle AOB, the angle AOE = x/2. Then from the right triangle AOE, we have: OA = R = (AB/2)/sin(x/2).
Triangle AEO is rectangular with right angle AEO. Since the height TH is also the bisector of the angle AOB, the angle AOE = x/2. Then from the right triangle AOE, we have: OA = R = (AB/2)/sin(x/2).