You will need
- - the radius of the circle:
- - the length of the arc of the chord;
- - angle of the arc of the chord;
- paper and drawing tools.
Instruction
1
Follow the drawing in accordance with the conditions of the problem. Draw a circle of a given radius. If you know the angle of the arc which subtends a chord, build it. Swipe radius, put a protractor to the desired angle and do another. The point of intersection of the radii with the circumference of connect direct. This will be the desired chord. If the angle is unknown, draw a random chord.
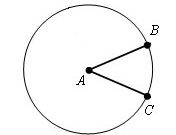
2
Follow these additional construction. Divide the chord in half and flick to this point, the perpendicular from the centre of the circle. You get an isosceles triangle, the altitude of which is perpendicular to the middle of the chord.
3
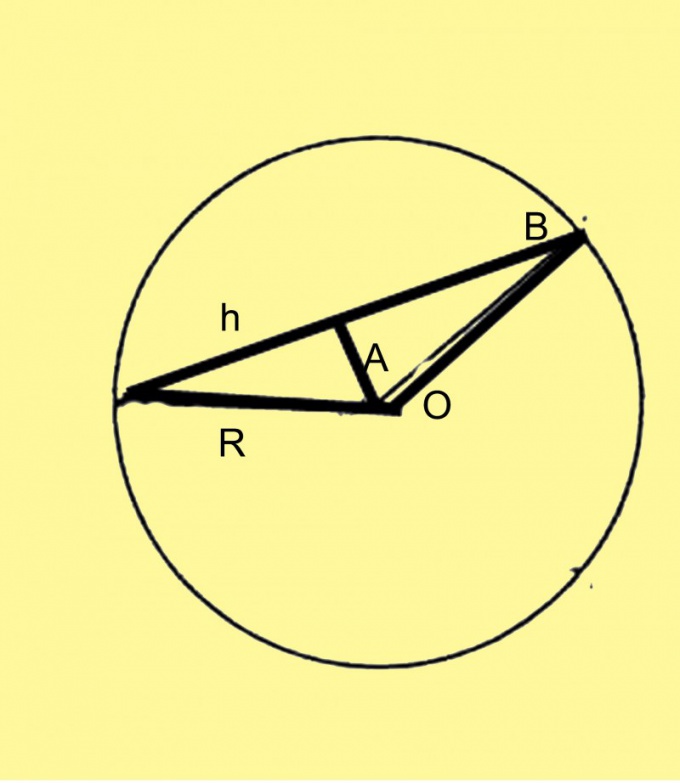
Label the radius as R, the chord - like h, and the Central angle A. Then h is fashionable to calculate using either the sine or cosine through. In the first case the formula will look like h=2R*sinA/2, where R is the known radius of the circle. In the second case the formula will look like h=R*√(1-cosB).
4
One of the most ancient geometric problems - to find the length of chord if you know the radius of a circle and arc length. Calculate the length of the circle P. It is equal to twice the radius multiplied by the factor P it can be expressed by the formula P=2PR.
5
Calculate the ratio of a given arc length l to the circumference P. This way you calculate the size of the arc angle. In this case, it can be in degrees or radians. Knowing the size, compute the sine of half-angle. Then you can calculate the size of the chord on the already known formula.
6
Often faced with the opposite task - for example, find the arc length and the radius of the circle and the chord length. Using theorem of sines, calculate the size of the half, and then an entire Central angle. Knowing him, the ratio of arc length to the circumference, calculate the unknown length of the arc.
Useful advice
With the longest chord is the diameter, usually act differently. Of course, it is possible for these ratios to calculate it, but the angle is known in advance and is 180°. In this case, sinA/2=sin90°=1. Accordingly, h=2R*sinA/2=2R.
When calculating the size of any direct way or another connected with the circumference, it is advisable to finish the drawing so as to obtain triangles whose parameters are known. In the case of chord you have used several properties of the line. For example, the fact that the perpendicular drawn to the chord from the center of the circle divides the chord in half.
When calculating the size of any direct way or another connected with the circumference, it is advisable to finish the drawing so as to obtain triangles whose parameters are known. In the case of chord you have used several properties of the line. For example, the fact that the perpendicular drawn to the chord from the center of the circle divides the chord in half.