How to find the incenter

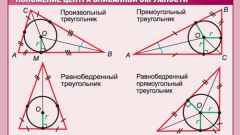
Find the center of the inscribed circle means to determine its position relative to the top individual angle or angles of the polygon. Remember, where is the center of a circleinscribed in a corner. It lies on the bisector. Construct angle of a given size and divide it in half. The radius of the inscribed circle you know. Have inscribed circles he is also the shortest distance from the center to the tangent, i.e. the perpendicular. The tangent in this case is the side angle. Build to one side the perpendicular is equal to the given radius. Ultimate point must lie on the bisector. You got a right triangle. Name it, for example, OSA. O is the vertex of the triangle and the center of the circle, OC is a radius, and OA — cut bisector. The angle CCA is equal to half the original angle. By theorem of sines, find the segment OA, which is the hypotenuse.

To determine the location of the center of the inscribed circle in the polygon and do the same build. Sides of any polygon, by definition, are tangent to the inscribed circle. Accordingly, the radius drawn to any point of tangency will be perpendicular to it. In the triangle center of inscribed circle is the intersection of the bisectors, i.e. the distance from the corners is determined in exactly the same way as in the previous case.

A circle inscribed in a polygon is simultaneously inscribed in every corner. It follows from its definition. Accordingly, the distance of the center from each vertex can be calculated similarly as in the case of a single angle. This is especially important to remember if you're dealing with the wrong polygon. In calculations of the rhombus or square enough to hold the diagonal. The center will coincide with the point of their intersection. To determine its distance from the vertices of the square by using the Pythagorean theorem. In the case of the rhombus is valid the theorem of sines or of the cosines, depending on which angle you are using for calculations.