Instruction
1
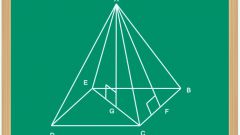
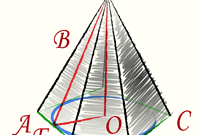
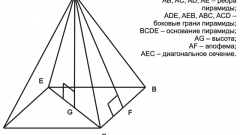
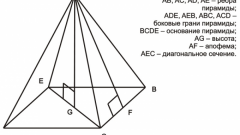
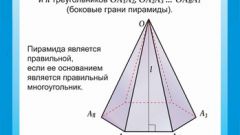
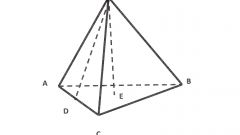
The total surface area of any polyhedron is the sum of the areas of its faces. In a regular quadrangular pyramid there are two forms of the polygons in the base has a square, the sides have a triangular configuration. Start calculations, e.g. calculation of the area of the quadrangular base of the pyramid (Sₒ). By definition, the right of the pyramid at its base must lie a regular polygon, in this case a square. If in terms of the length of an edge of (a), just erect it in the second degree: Sₒ = a2. If you know only the length of the diagonal of the base (l), to compute the area find the half of its square: Sₒ = l2/2.
2
Determine the area of the triangular lateral faces of the pyramid Sₐ. If you know the length of its shared base edge (a) and apofema (h), calculate half of the product of these two quantities: Sₐ = a*h/2. Under these conditions, the lengths of a side edge (b) and fin base (a) find half of a work the length of its base at the root of the difference between the squared length of a side edge and a quarter of square base length: Sₐ = ½*a*√(b2-a2/4). If in addition the length of the common base edge (a) given a plane angle at the vertex of the pyramid (α), calculate the ratio of the squared length of the edge to twice the cosine of half the plane angle: Sₐ = a2/(2*cos(α/2)).
3
Calculating the area of one side face (Sₐ), increase the value four times to calculate the lateral surface area of the regular quadrangular pyramid. At a certain apofema (h) and the perimeter of the base (P) is the action along with all the previous step can be replaced by calculating half the product of these two parameters: 4*Sₐ = ½*h*P. In any case, the lateral surface area will add up to calculated in the first step, with an area of square base figures - this will be the total surface area of a pyramid: S = Sₒ+4*Sₐ.