Instruction
1
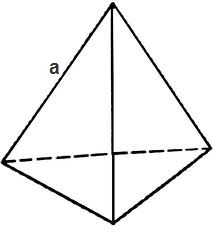
To find the surface area of the tetrahedron, it is necessary to calculate the area of a triangle which constitutes its face.
If the triangle is equilateral, its area is equal to
S = √3 * 4 / a2, where a is an edge of a tetrahedron
then the surface area of the tetrahedron is given by
S = √3 * a2.
If the triangle is equilateral, its area is equal to
S = √3 * 4 / a2, where a is an edge of a tetrahedron
then the surface area of the tetrahedron is given by
S = √3 * a2.
2
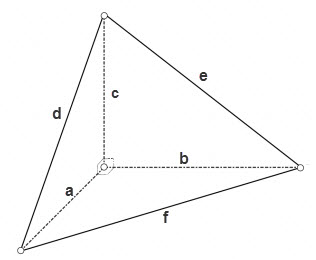
If the tetrahedron is rectangular, i.e. all the flat corners with one of its vertices are straight, square, three faces are rectangular triangles can be calculated by the formula
S = a * b *1/2,
S = a * c *1/2,
S = b * c *1/2,
the area of the third face can be calculated by one of General formulas for triangles, for example, by Heron's formula
S = √(p * (p - d) * (p - e) * (p - f)), where p = (d + e + f)/2 – properiter triangle.
S = a * b *1/2,
S = a * c *1/2,
S = b * c *1/2,
the area of the third face can be calculated by one of General formulas for triangles, for example, by Heron's formula
S = √(p * (p - d) * (p - e) * (p - f)), where p = (d + e + f)/2 – properiter triangle.
3
In General, the area of each tetrahedron can be calculated using Heron's formula to calculate the area of each face.


