You will need
  • - a geometric solid with specified parameters;
  • and measuring devices;
  • formula to calculate area of geometric shapes.
Instruction
1
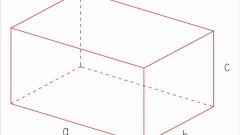
If you want to calculate the surface area of the rectangular floor of a room or of a rectangular plot of land, measure their length and width. The results multiply. In this case, the surface area is calculated by the formula S=ab, where S is the surface area, a and b are the sides of the rectangle. The formula for the area of a square would look like S=a2.
2
If the planar surface has a more complex form, it must be divided into more simple parts of formulas for calculating the area of which you are aware. For example, irregular polygon can be divided into several triangles or triangles and a rectangle. In this case, consider the given in terms of the problem parameters of the polygon.
3
If you are not dealing with plane figures and geometric bodies need to operate exactly the same. In terms of tasks usually set the parameters of the figure to be built or to calculate. Please read carefully, what kind of area you need to find. Almost every geometrical body has the total surface area, lateral surface area and area of one or two bases.
4
Calculate the area of the grounds. The cone and pyramid base one. The base of the pyramid is a polygon and is calculated by relevant formula. The square base of a regular quadrangular pyramid calculate by formula the area of a square, that is elevating to the square the length of one of its sides. If the base of the pyramid lies a complex polygon, divide it into more simple with the known parameters. At the base of the cone is the circle, and accordingly, the area is calculated by the formula S=πR2.
5
Find the lateral surface area. At cuboid it is calculated according to the formula S=p*h, where p is the perimeter of the rectangle of the base and h is the height. The surface area of a cube is calculated by the formula S=4a2, since the lateral surface consists of 4 squares.
6
For the calculation of the conical surface is most convenient to do a scan. Find the length of a circle given its radius. It will be equal to the arc length of the lateral surface of the cone. The length of an arc calculate the Central angle, then the radius of the circle sector which is the lateral surface of the cone. Knowing these values, find the area of a sector, that is, the lateral surface area of a cone.
7
To determine the full surface or other geometric bodies add together the square of the lateral surface and bases.