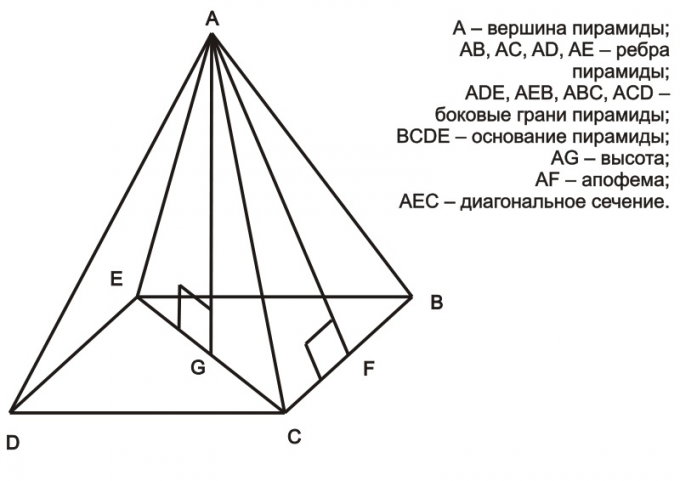
Instruction
1
First of all, it should be understood that the lateral surface of the pyramid is represented by several triangles, the square of which can be found through a variety of formulas, depending on known data:
S = (a*h)/2, where h is the height lowered on the side of a;
S = a*b*sinβ, where a, b are the sides of a triangle, and β is the angle between these sides;
S = (r*(a + b + c))/2, where a, b, c be the sidelengths of triangle and r is the radius of the inscribed in the triangle circumference;
S = (a*b*c)/4*R, where R is the radius of the circle circumscribed around the triangle;
S = (a*b)/2 = r2 + 2*r*R (if the triangle is rectangular);
S = S = (a2*√3)/4 (if the triangle is equilateral).
In fact, it is only the most basic of well-known formulas for finding the area of a triangle.
S = (a*h)/2, where h is the height lowered on the side of a;
S = a*b*sinβ, where a, b are the sides of a triangle, and β is the angle between these sides;
S = (r*(a + b + c))/2, where a, b, c be the sidelengths of triangle and r is the radius of the inscribed in the triangle circumference;
S = (a*b*c)/4*R, where R is the radius of the circle circumscribed around the triangle;
S = (a*b)/2 = r2 + 2*r*R (if the triangle is rectangular);
S = S = (a2*√3)/4 (if the triangle is equilateral).
In fact, it is only the most basic of well-known formulas for finding the area of a triangle.
2
Calculating using the above formulas the area of all the triangle faces of the pyramid, you can begin calculating the square of the side surface of the pyramid. This is done very simply: you add together the area of all triangles forming the lateral surface of the pyramid. The formula can be expressed as:
SN = ΣSi, where SN is the lateral surface area of a pyramid, Si - the area of the ith triangle as part of its side surface.
SN = ΣSi, where SN is the lateral surface area of a pyramid, Si - the area of the ith triangle as part of its side surface.
3
For clarity, we can consider a small example: given a right pyramid, the side faces of which is formed by the equilateral triangles and base is square. The edge length of the pyramid is 17 cm you want to find the lateral surface area of the pyramid.
Solution: a known edge length of the pyramid, we know that her face is an equilateral triangle. Thus, we can say that all sides of all triangles of the side surface is equal to 17 cm is Therefore in order to calculate the area of any of these triangles, you will need to use the formula:
S = (172*√3)/4 = (289*1.732)/4 = 125.137 cm2
It is known that at the base of the pyramid is a square. Thus, it is clear that these equilateral triangles four. Then the lateral surface area of a pyramid is calculated as follows:
125.137 cm2 * 4 = 500.548 cm2
Answer: the lateral surface area of a pyramid is 500.548 cm2
Solution: a known edge length of the pyramid, we know that her face is an equilateral triangle. Thus, we can say that all sides of all triangles of the side surface is equal to 17 cm is Therefore in order to calculate the area of any of these triangles, you will need to use the formula:
S = (172*√3)/4 = (289*1.732)/4 = 125.137 cm2
It is known that at the base of the pyramid is a square. Thus, it is clear that these equilateral triangles four. Then the lateral surface area of a pyramid is calculated as follows:
125.137 cm2 * 4 = 500.548 cm2
Answer: the lateral surface area of a pyramid is 500.548 cm2