Instruction
1
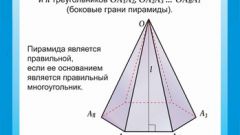
Pyramid
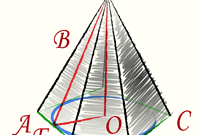
All lateral edges are equal, the side faces are isosceles triangles are equal, and the base is a regular polygon. Because all apodeme of a regular pyramid are equal, then it is sufficient to find one in any triangle. The triangles are isosceles, and apofema is the height. Height conducted in an isosceles triangle from the vertex to the base is the median and the angle bisector. The median divides the side in half, and bisects the angle into two equal angles. Height – the perpendicular drawn from the apex to the base.
All lateral edges are equal, the side faces are isosceles triangles are equal, and the base is a regular polygon. Because all apodeme of a regular pyramid are equal, then it is sufficient to find one in any triangle. The triangles are isosceles, and apofema is the height. Height conducted in an isosceles triangle from the vertex to the base is the median and the angle bisector. The median divides the side in half, and bisects the angle into two equal angles. Height – the perpendicular drawn from the apex to the base.
2
For example, know all the sides of an isosceles triangle and the median, which divides the base into two equal segments. Since the median is an altitude, it is perpendicular, i.e. the angle between the midpoint and the base is 90 degrees. So, it turns out a right triangle. Side is the hypotenuse, half the base and height(median) is the legs. The Pythagorean theorem States: the square of the hypotenuse is equal to the sum of the squares of the other two sides. This way you can find the height.
3
Let a known angle, lying opposite the base. And any one side (either the side or the base). Bisector drawn from the vertex to the base, is the height. So again, is a right triangle. Known angle and one side. Using sine, cosine and tangent to find the height. Sine – the ratio of the opposite leg to the hypotenuse, the side - ratio of the adjacent leg to the hypotenuse tangent is the ratio of sine to cosine, or opposite over adjacent. Substituting the known sides, calculate the height.
The lateral surface area of a regular pyramid equals half the product of the perimeter of the base to the apofema.
The lateral surface area of a regular pyramid equals half the product of the perimeter of the base to the apofema.
4
The right truncated pyramid
Lateral faces – regular trapezoid. The lateral edges are equal. Apofema – height held in the line. Let there are two bases and the lateral edge. From the top are height so that on a larger basis, they cut off a rectangle. Then, if you mentally remove the rectangle will remain isosceles triangle, the height of which can be found by the first method. If you know the obtuse angles of the trapezoid, then during the height, subtract the angle equal 90 degrees(because the altitude is the perpendicular)from stupid. Then will be known the acute angle in the triangle. Height or apofema again, you can find 1 way.
Lateral faces – regular trapezoid. The lateral edges are equal. Apofema – height held in the line. Let there are two bases and the lateral edge. From the top are height so that on a larger basis, they cut off a rectangle. Then, if you mentally remove the rectangle will remain isosceles triangle, the height of which can be found by the first method. If you know the obtuse angles of the trapezoid, then during the height, subtract the angle equal 90 degrees(because the altitude is the perpendicular)from stupid. Then will be known the acute angle in the triangle. Height or apofema again, you can find 1 way.