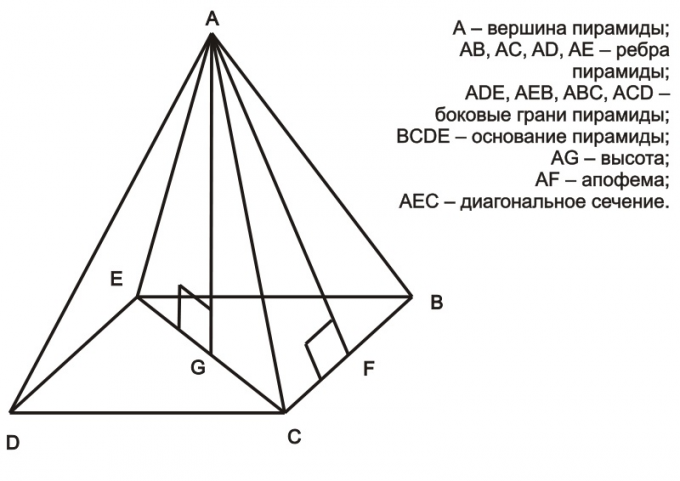
You will need
- Depending on the situation, to know the volume of a pyramid, the area of the lateral faces of the pyramid, the edge length the length of the diameter of the polygon at the base.
Instruction
1
One of the ways to find the height of the pyramid, and not only right is to Express it through the volume of the pyramid. The formula, with the help of which you can find out its volume, is as follows:
V = (S*h)/3, where S is the area of all the lateral faces of the pyramid in the sum, h is the height of the pyramid.
Then from this formula we can deduce another, to find the height of the pyramid:
h = (3*V)/S
For example, it is known that the area of the lateral faces of the pyramid 84 cm2, and the volume of a pyramid is equal to 336 cubic cm, Then find the height :
h = (3*336)/84 = 12 cm
Answer: the height of the pyramid is 12 cm
V = (S*h)/3, where S is the area of all the lateral faces of the pyramid in the sum, h is the height of the pyramid.
Then from this formula we can deduce another, to find the height of the pyramid:
h = (3*V)/S
For example, it is known that the area of the lateral faces of the pyramid 84 cm2, and the volume of a pyramid is equal to 336 cubic cm, Then find the height :
h = (3*336)/84 = 12 cm
Answer: the height of the pyramid is 12 cm
2
Considering the right pyramid, the base of which is a regular polygon, we can conclude that the triangle formed by the height, half the diagonal and one of the faces of the pyramid is a right triangle (e.g., triangle AED in the figure above). According to the Pythagorean theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides (a2 = b2 + c2). In the case of the right pyramid, the hypotenuse is the face of the pyramid, one of the legs is half the diagonal of the polygon at the base and the other leg is the height of the pyramid. In this case, given the length of edges and diagonals, we can calculate the height. As an example we can consider the triangle AEG:
AE2 = EG2+GA2
Here the height of pyramid GA can be expressed as:
GA = √(AE2-EG2).
AE2 = EG2+GA2
Here the height of pyramid GA can be expressed as:
GA = √(AE2-EG2).
3
To make it more clear how to find the height of a regular pyramid, you can see an example: in the right pyramid of edge length 12 cm, diagonal length of the polygon at the base is 8 cm Based on these data, it is required to find the length of the height of the pyramid.Solution: 122 = 42 + c2, where C is the unknown side (height) of the pyramid (a right triangle).
144 = 16 + 128
Thus, the height of the pyramid √128, or about 11.3 cm
144 = 16 + 128
Thus, the height of the pyramid √128, or about 11.3 cm