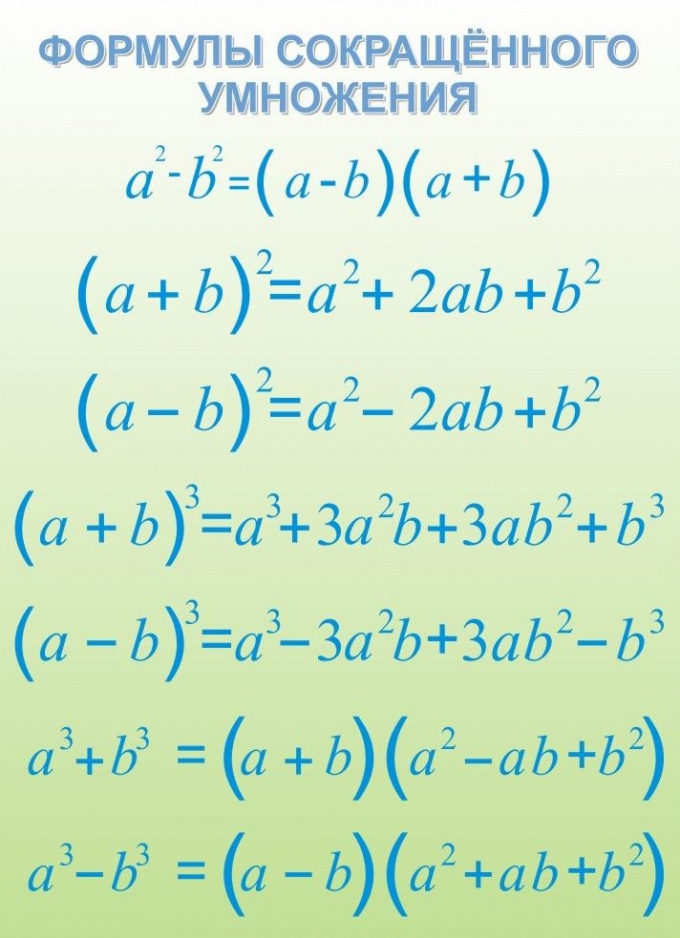How to simplify an expression

If the terms are monomials with the same multipliers, find the sum of coefficients in front of them and multiply by a common set of multipliers. For example, if you have the expression 2•a-4•a+5•a+a=(2-4+5+1)∙a=4∙a.

To simplify expressions, use formulas of reduced multiplication. The most popular include the squared difference, difference of squares, difference and sum of cubes. For example, if there is an expression 256-384+144, visualize it as 162-2•16•12+122=(16-12)2=42=16.

In that case, if the expression is a natural fraction, select from the numerator and denominator a common factor and reduce a fraction on it. For example, if you need to reduce the fraction (3•a2-6•a•b+3•b2)/(6∙a2-6∙b2), take out from the numerator and denominator for common factors in the numerator it will be 3 in denominator of 6. Get the expression (3•(a2-2•a•b+b2))/(6∙(a2-b2)). Reduce the numerator and the denominator by 3 and apply to the remaining expressions are formulas of reduced multiplication. The numerator is the squared difference, and for the denominator a difference of squares. Get the expression (a-b)2/(2∙ (a+b)∙(a-b)) reducing it by a common factor a-b, obtain an expression (a-b)/(2∙ (a+b)), which, when specific values of the variables is much easier to calculate.

If the monomials have the same multiplier raised to a power, that when they are totaled, ensure the degree was equal, otherwise impossible to reduce these. For example, if you have the expression 2∙m2+6•m3-m2-4•m3+7, when such information will m2+2•m3+7.

When simplifying trigonometric identities use formulae for their conversion. The main trigonometric identity sin2(x)+cos2(x)=1, sin(x)/cos(x)=tg(x), 1/ tg(x)= ctg(x), the formulas sum and difference of arguments, double, triple, argument and other. For example, (sin(2∙x)- cos(x))/ ctg(x). Shall describe the formula for the double argument and cotangent, as the relationship of cosine to the sine. Get (2∙ sin(x)• cos(x) cos(x))• sin(x)/cos(x). Take out a common factor, cos(x) and simplify the fraction cos(x)•(2∙ sin(x) - 1)• sin(x)/cos(x)= (2∙ sin(x) - 1) • sin(x).