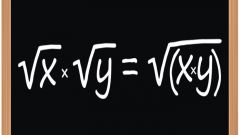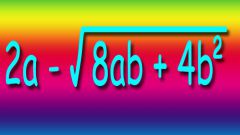How to solve examples with roots

The root of degree n of the number called is a number that when raised to a this degree will give the number from which to extract the root. Most often, actions are performed with the square roots, which correspond to 2 degrees. At root it is often impossible to find it explicitly, and the result is a number that cannot be expressed in the form of a genuine fraction (transcendental). But using some techniques, we can greatly simplify the solution of examples with roots.

You will need

- the notion of root of a number;
- actions with degrees;
formulas of reduced multiplication;
calculator.

Instruction

If you do not need absolute accuracy, while solving examples with the roots use a calculator. To extract the number of the square root, enter it on the keyboard, and just press the relative button, which shows the sign of the root. As a rule, calculators, take the square root. But for calculation of roots of higher degrees, use of a number raised to the degree (engineering calculator).

To extract the square root raise to the power 1/2, cubic root of 1/3, and so on. In this case you must keep in mind that when extracting the roots of even degree, the number must be positive, otherwise the calculator will not just give the answer. This is due to the fact that during the construction in even degree any number will be positive, for example, (-2)^4=(-2)∙ (-2)∙ (-2)∙ (-2)=16. To extract the square root evenly, when possible, use the table of squares of natural numbers.

If not near a calculator, or require absolute precision in the calculations use properties of roots and various formulas to simplify expressions. Many of the numbers, you can remove the root part. To do this, use the property that the root of the product of two numbers is equal to the product of the roots of these numbers √m * n=√m∙√n.

Example. Calculate the value of the expression (√80-√45)/ √5. Direct calculation will give nothing, because evenly is not removed no root. Convert the expression (√16∙5-√9∙5)/ √5=(√16∙√5-√9∙√5)/ √5=√5∙(√16-√9)/ √5. Perform a reduction of the numerator and denominator by √5, get (√16-√9)=4-3=1.

If the radical expression or the root raised to the power, when you root, use the property that the exponent radical expressions can be divided into the degree of the root. If the division is performed evenly, the number is entered from under the root. For example, √5^4=52=25.

Example. To calculate the value of the expression (√3+√5)∙(√3-√5). Apply the formula of difference of squares and get the (√3)2-(√5)2=3-5=-2.

Is the advice useful?