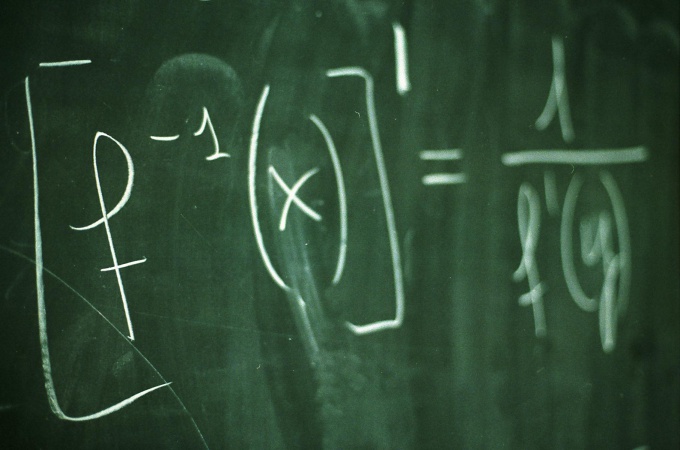You will need
  • Knowledge of the rules of converting fractions
Instruction
1
The most trivial transformation is a simple flipping of a fraction or a permutation of the numerator and denominator swapped. The result is a number, reverse the source and the product of these two numbers will give the unit. Example: (2/5)*(5/2) = 1.
2
As you can see from the previous example, if you divide a unit into any number we get the number back to him. But divide the number of units a number is a number x to the power of -1. Therefore, (x/y) = (y/x)^(-1). Example: (2/3) = (3/2)^(-1).
3
Sometimes, the calculations can get cumbersome, "multistoried" fraction. To simplify a fraction they also need to turn. Turn these fractions according to the following rules: x/(y/c) = (x*c)/y (x/y)/c = x/(y*c), (x/y)/(b/c) = (x*c)/(y*b).
4
It is useful to change the type of shot and in the case where in the denominator there is an irrational number. To do this, the numerator and denominator of this fraction must be multiplied by is an irrational number. Then an irrational number will be in the numerator of the fraction. Example: 1/sqrt(2) = sqrt(2)/(sqrt(2)*sqrt(2)) = sqrt(2)/2.Source: Maths: a Big book reference for students and University entrants", D. I. Averyanov, P. I. Altynov, I. I. Bavrin., 1998