Instruction
1
Note the example given on the sheet. If it is a polynomial highlight in this General part. To do this, find all terms with the same base. The same base members with the same literal part and also with one degree. Such terms are called similar.
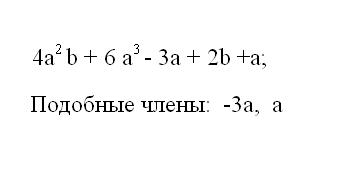
2
Fold such members. In this case, consider the signs ahead of them. If before one of them is the " - " sign instead of addition perform subtraction of members and subject to the same sign, write down the result. If the sign "-" are both members, therefore, you perform an addition and the result is also written with the sign "-".
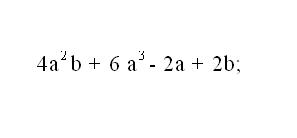
3
In the presence of fractional values as coefficients of a polynomial, give to simplify the sample fractions to a common denominator. To do this, multiply all the coefficients of the expression for the same number so that when reducing fractions, leaving only the integer part. In the simplest case, the common denominator is the product of all denominators in fractional coefficients. After multiplying all the members, guide the facilitation of such events.
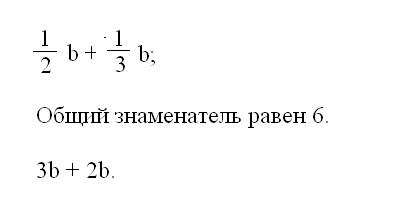
4
After bringing to a common denominator and combine like terms take out a common subexpression in parentheses. To do this, define the group members, where has the same subexpression. Divide the coefficients of the group on the General part and put it in front of the brackets. In parentheses Express not the whole polynomial, namely the group members with the remainder from dividing the coefficients.
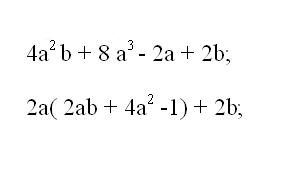
5
Don't lose the sign during the removal of the brackets. If you want the common part to stand with the sign "-", then for each member in brackets will change the sign to opposite. The other members not parties to the removal of the brackets, write before or after the parentheses, preserving their sign.
6
If the brackets imposed a General part of the degree, for the group in parenthesis is a subtraction of index unbearable degree. When opening brackets extent such members are added and coefficients are multiplied.
7
The expression can be reduced to an integer, if it divided all the coefficients of the polynomial. Check, or in the given example, the common divisor. To do this, locate all of the coefficients of the number that evenly share each of them. Follow division all coefficients of the polynomial.
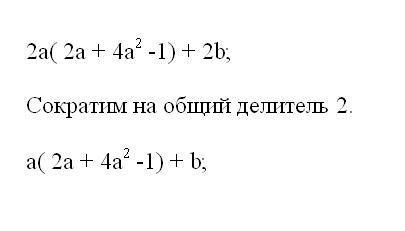
8
If the example is set to a literal of the variable, substitute it in the converted expression. Count and record the result. An example is solved.