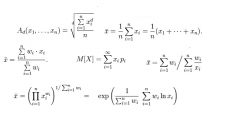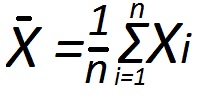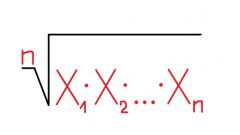Instruction
1
The average arithmetic mean of a set of numbers is defined as their sum divided by their number. The sum of all numbers of the set divided by the number of numbers in this set.The most simple case is to find the arithmetic mean of two numbers x1 and x2. Then their arithmetic mean X = (x1+x2)/2. For example, X = (6+2)/2 = 4 - the arithmetic mean of the numbers 6 and 2.
2
The General formula for finding the arithmetic mean of the n numbers would look like this: X = (x1+x2+...+xn)/n. It can also be written as: X = (1/n)?xi, where the summation is for index i from i = 1 to i = n.For example, the arithmetic mean of three numbers X = (x1+x2+x3)/3, five numbers is (x1+x2+x3+x4+x5)/5.
3
Interest is the situation when the set of numbers represents the members of an arithmetic progression. As you know, members of the arithmetic progression is a1+(n-1)d, where d is the step of progression and n is the number of the member of progression.Let a1, a1+d, a1+2d,..., a1+(n-1)d - members of an arithmetic progression. Their arithmetic mean is equal to S = (a1+a1+d+a1+2d+...+a1+(n-1)d)/n = (na1+d+2d+...+(n-1)d)/n = a1+(d+2d+...+(n-2)d+(n-1)d)/n = a1+(d+2d+...+dn-d+dn-2d)/n = a1+(n*d*(n-1)/2)/n = a1+dn/2 = (2a1+d(n-1))/2 = (a1+an)/2. Thus the arithmetic mean of members of an arithmetic progression is equal to the arithmetic mean of its first and last members.
4
It is also true the property that each member of an arithmetic progression is equal to the average between the previous and the next member of the progression: an = (a(n-1)+a(n+1))/2 where a(n-1), an, a(n+1) successive members of the sequence.
Note
To find the arithmetic mean of several numbers is to be folded between them. Thereafter, the resulting amount will be divided by the number of terms. To make it clearer, let's look at how to find average of numbers, for example: 78, 115, 121 and 224. The arithmetic mean of several numbers found using Excel.
Useful advice
The calculated value is called arithmetic average or just average. Definition. The average of several numbers is the number equal to the ratio of the sum of these numbers to their number. Not only arithmetic mean shows where on the number line are the numbers of some set. Another indicator is the median a number that separates this set into two parts of equal size. Explain with examples how to find the median of various sets of numbers.