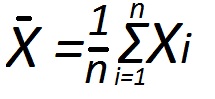Instruction
1
The first is to understand how this formed the sample average. For example, given some set of numeric values that consists of n units. All these units form the so-called sample. The sum of all these numbers is a formula to be expressed as ΣXi (Xi is any of the values of this sample, where i = 1,2,3...i-1,i. That is, i is the number of values in the sample). Then, in order to find the sample mean, you add together all the values from the sample and divided by their number n.
2
On top of all the recorded data can be expressed by only one formula, which is listed above. The sample mean is the simplest of the characteristics that reveal the nature of the sampling. It is widely used in mathematical statistics, probability theory, and also in many other fields of knowledge.
3
In the school curriculum is not given any formulas for finding average, although it becomes immediately clear that when children in math class in 5th grade are asked to find the average value of any numbers the children already know in order to find the average of these numbers, they will need to fold them all and then divided by their number. In fact, they also find the sample mean.
Note
When you look at the formula for the sample mean, then I am immediately reminded of course of school mathematics in which it was necessary to find an arithmetic mean. Indeed, the formula is almost identical, but from a mathematical point of view while the sample mean is not considered some kind of preset already set (as given in the book of problems in mathematics), and the space in which there are many random values. Exploring this space is some kind of sampling frame, from which subsequently is the sample mean.