Instruction
1
Integration is an operation which is the opposite of differentiation. So, if you want to learn how to integrate, you first need to learn to find from any of the functions of derivatives. You can learn it quickly enough. After all, there is a special table of derivatives. It is already possible to solve simple integrals. And there are the table of basic indefinite integrals. It is presented in the figure.
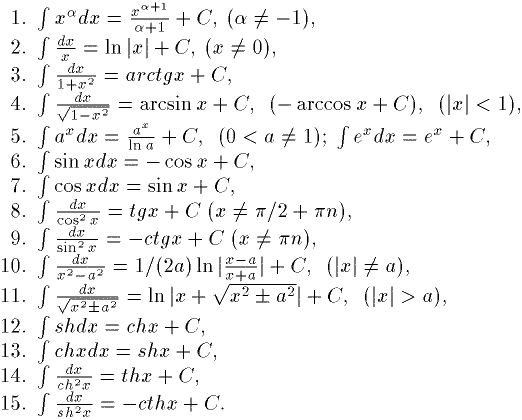
2
Now we need to remember the most basic properties of integrals, given below.
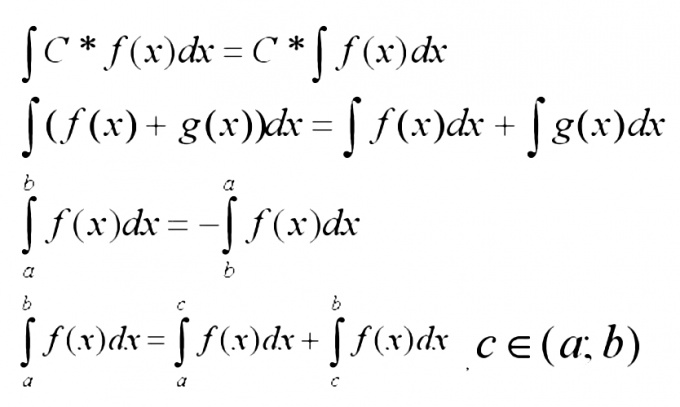
3
Integral of sum of functions is best decomposed into a sum of integrals. This rule most often applies when the components function is fairly simple, if you can find them using the table of integrals.
4
There is one very important method. According to this method the function must be paid under the differential. They are especially good to use if before you make a differential, of a function take the derivative. Then it is put instead of dx. In that way we get df(x). This way you can easily ensure that even function under the differential can be used as an ordinary variable.
5
Another basic formula, without which very often just not do - this is the formula of integration by parts: Integral(udv)=uv-Integral(vdu). This formula is effective in the case if in the task it is required to find the integral of the product of two elementary functions. Of course you can use regular conversion, but it is difficult and time consuming. Therefore, to take the integral with the help of this formula is much simpler.
Useful advice
To solve the integral means to integrate in the variable set function. If the standard integral, we can say that it is almost solved. If he has a more complicated entry is main task when finding the integral of a function becomes bringing it to tabular form.