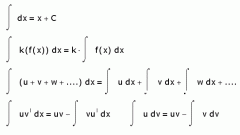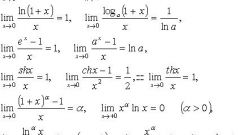Instruction
1
Integration is the inverse operation of differentiation. Therefore, in order to integrate, you need to be able to take derivatives of any functions. Learn this easy: there is a table of derivatives, knowing which to integrate simple functions is quite simple.
2
The integration of the sum of some functions can always be represented as a sum of integrals. To use these rules particularly useful when the functions themselves are simple and can be calculated by the table of basic indefinite integrals below.
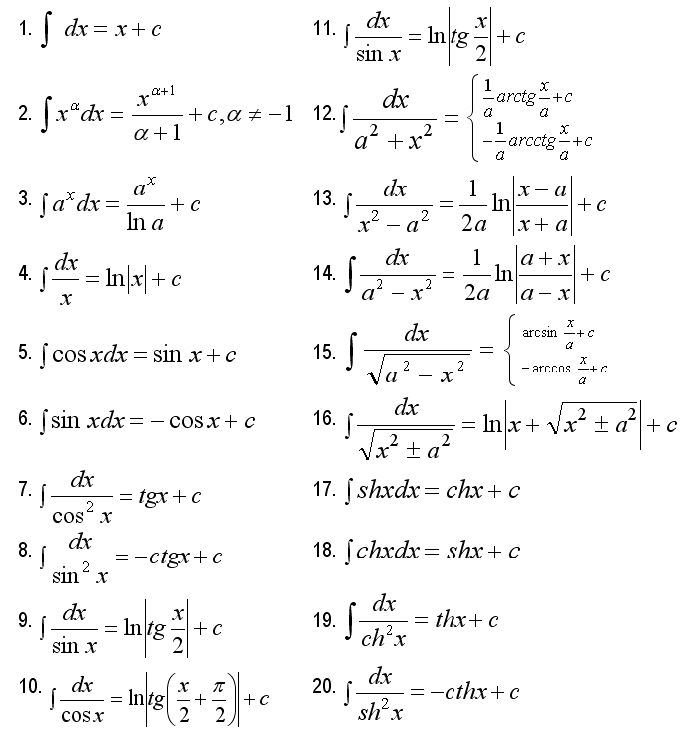
3
A very important method - integration by the method of any functions under the differential. She especially convenient to use when making the differential under - we take the derivative of the function and put it in place of dx (that is, we have df(x)'), we obtain that the function under the differential we use as a variable.
4
Another basic formula: Integral(udv)=uv-Integral(vdu) will help us in the case when we are faced with the integral of the product of two elementary functions. To take the integral when it is much simpler than using convert.