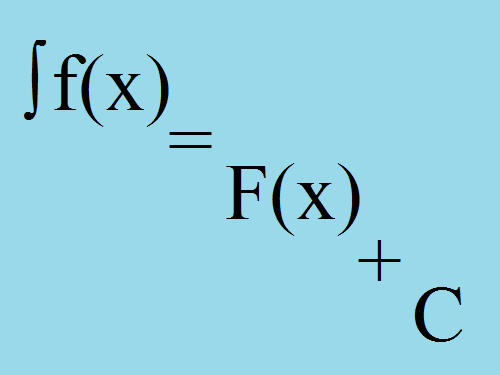How to find the integral

Integral refers to the concepts of mathematical analysis and graphically represents the area of a curvilinear trapezoid, bounded on the x-axis limit integration points. Find the integral of the function is much more complicated than finding its derivative.

There are several methods of evaluating of indefinite integrals: direct integration, the introduction under the sign of the differential, the substitution method, integration by parts, substitution Weierstrass, the theorem of Newton-Leibnitz etc.

Direct integration involves bringing through simple transformations of the original integral to a tabular value. Example:∫dy/(sin2y·cos2y) = ∫(cos2y + sin2y)/(sin2y·cos2y)dy = ∫dy/sin2y + ∫dy/cos2y = -ctgy + tgy + C.

Method of introducing, under the sign of the differential or the change of variable is a new variable. The original integral is reduced to a new integral which can be converted to the tabular view by a direct integration:suppose we have the integral ∫f(y)dy = F(y) + C and a variable v = g(y), then:∫f(y)dy -> ∫f(v)dv = F(v) + C.

Keep in mind some simple substitutions to ease working with this method:dy = d(y + b) ydy = 1/2·d(y2 + b);sinydy = - d(cosy);cosydy = d(siny).

Пример:∫dy/(1 + 4·y2) = ∫dy/(1 + (2·y) 2) = [dy -> d(2·y)] = 1/2·∫d(2·y)/(1 + (2·y) 2) = 1/2·arctg2·the + C.

Integration by parts is performed according to the following formula:∫udv = u·v - ∫vdu.Example:∫y·sinydy = [u = y; v = siny] = y·(cosy) – ∫(-cosy)dy = -y·cosy + siny + C.

Definite integral in most cases is the theorem of Newton-Leibnitz:∫f(y)dy on the interval [a; b] is equal to F(b) – F(a).Example: Find ∫y·sinydy on the interval [0; 2π]:∫y·sinydy = [u = y; v = siny] = y·(cosy) – ∫(-cosy)dy = (-2π·cos2π + sin2π) – (-0·cos0 + sin0) = -2π.