You will need
- - computer with installed application MS Excel;
- table specified function.
Instruction
1
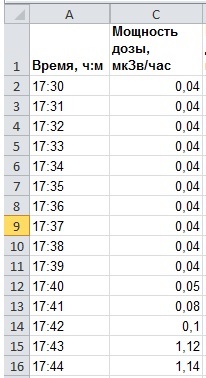
Let's say we have a table given a certain value. For example, let it be the accumulated dose of radiation during air travel. Let's say there was such an experiment: a man with a dosimeter was on a plane from point A to point B, and periodically measured dosimeter dose rate (measured in microsieverts per hour). You might is surprised, but in normal flight, the person receives a radiation dose 10 times higher than the background level. But the effect is transient and therefore not dangerous. Based on measurements we have a table like this format: Time - dose.
2
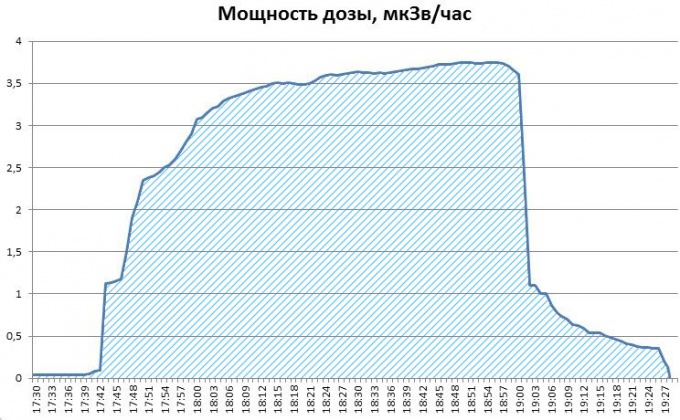
The essence of the method is that the definite integral is the area under the graph of the desired size. In our example, if the flight lasted almost 2 hours, from 17:30 to 19:27 (see the figure), to find the accumulated dose, it is necessary to determine the area of the shape under the graph of dose - schedule table predetermined value.
3
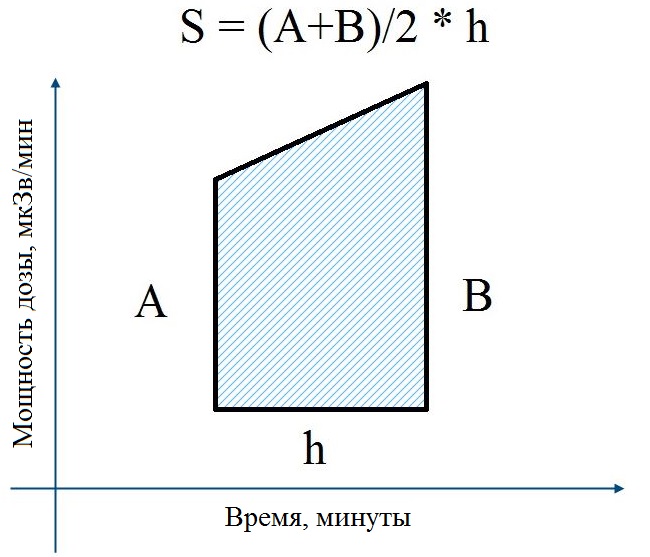
To calculate the integral we will be the most simple but quite accurate method - the method of trapezoids. Let me remind you, every curve can be divided into a trapezoid. The sum of the areas of these trapezoids and is the required integral.
Area of a trapezoid is defined simply: the sum of the bases multiplied by the height. The reason in our case is a tabular measured values of dose rate for 2 consecutive time interval, and the height is the difference of time between two measurements.
Area of a trapezoid is defined simply: the sum of the bases multiplied by the height. The reason in our case is a tabular measured values of dose rate for 2 consecutive time interval, and the height is the difference of time between two measurements.
4
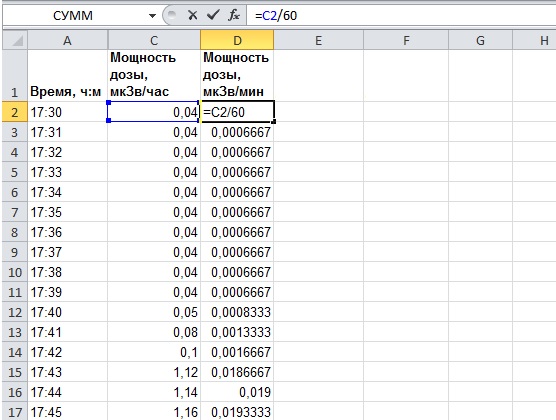
In our example of measuring the dose of radiation is given in µsv/h. Translate this in µsv/min, since the data are given with a frequency of 1 time per minute. It is necessary to harmonize units of measure. We can't take the integral over time measured in minutes from the value measured in hours.
For translation, simply divide the dose rate in µsv/h by the line 60. Add another column to our table. The illustration in column "D" in line 2, enter "=C2/60". And then using the fill handle (the mouse pull the black rectangle in the lower right corner of the cell) extend this formula to all cells in column "D".
For translation, simply divide the dose rate in µsv/h by the line 60. Add another column to our table. The illustration in column "D" in line 2, enter "=C2/60". And then using the fill handle (the mouse pull the black rectangle in the lower right corner of the cell) extend this formula to all cells in column "D".
5
Now we need to find area of trapezoids each time. In column "E" will be calculated by the above formula of the area of the trapezoids.
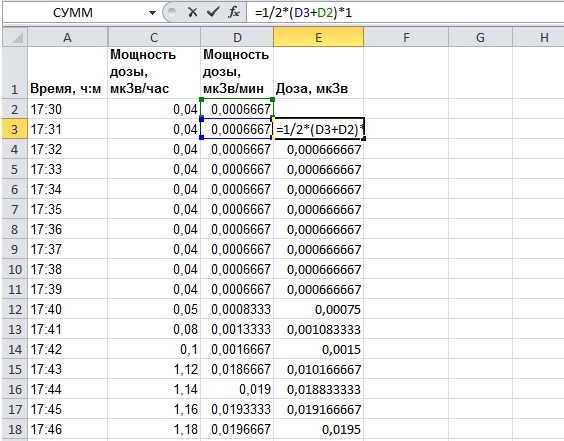
The sum of bases is half the sum of the two consecutive dose rate from column "D". As these go with a period of 1 time per minute, and we take the integral time, expressed in minutes, the height of each trapezoid is equal to one (time difference between each two consecutive measurements, for example, 17ч31м - 17ч30м = 0ч1м).
Get the formula in cell E3: "=1/2*(D2+D3)*1". It is clear that "*1" can not write, I did it just for the sake of completeness. The picture explains everything more clearly.
Similarly, using the fill handle distributed by formula to the whole column. Now in each cell of column "E" is calculated, the accumulated dose over 1 minute of flight.
The sum of bases is half the sum of the two consecutive dose rate from column "D". As these go with a period of 1 time per minute, and we take the integral time, expressed in minutes, the height of each trapezoid is equal to one (time difference between each two consecutive measurements, for example, 17ч31м - 17ч30м = 0ч1м).
Get the formula in cell E3: "=1/2*(D2+D3)*1". It is clear that "*1" can not write, I did it just for the sake of completeness. The picture explains everything more clearly.
Similarly, using the fill handle distributed by formula to the whole column. Now in each cell of column "E" is calculated, the accumulated dose over 1 minute of flight.
6
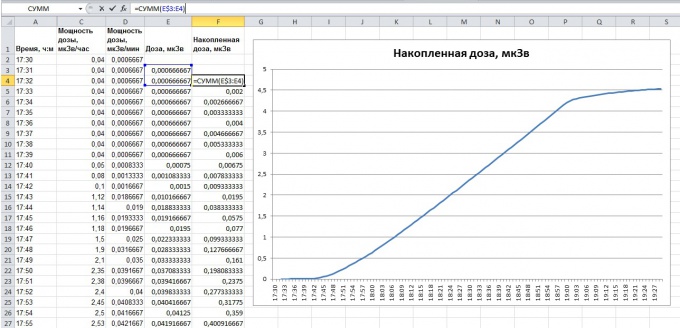
It remains to find the sum of the calculated squares, and trapezoids. In cell "F2" to write the formula "=SUM(E:E)", this is the desired integral is the sum of all values in column "E".
You can do a little bit more difficult to determine the accumulated dose at different points of the flight. To do this, in cell "F4" will enter the formula "=SUM(E$3:E4)" and fill handle will extend the entire column "F". The symbol "E$3" tells Excel what to change the index of the first cell, from which a score, it is not necessary.
We construct a graph in columns "F" and "A", i.e. the change in the accumulated dose of radiation in time. It is clearly seen the increase of the integral, as it should be, and the final value is accumulated over a two-hour flight radiation dose equal to approximately 4.5 microsievert.
Thus, we just found the definite integral of the given function table in Excel to a real physical example.
You can do a little bit more difficult to determine the accumulated dose at different points of the flight. To do this, in cell "F4" will enter the formula "=SUM(E$3:E4)" and fill handle will extend the entire column "F". The symbol "E$3" tells Excel what to change the index of the first cell, from which a score, it is not necessary.
We construct a graph in columns "F" and "A", i.e. the change in the accumulated dose of radiation in time. It is clearly seen the increase of the integral, as it should be, and the final value is accumulated over a two-hour flight radiation dose equal to approximately 4.5 microsievert.
Thus, we just found the definite integral of the given function table in Excel to a real physical example.