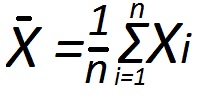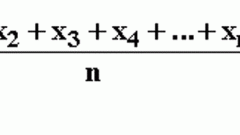You will need
- calculator.
Instruction
1
The variance in mathematical statistics and probability theory is defined as a measure of dispersion (deviation from average). The smaller the value of this index, the more uniform the set and in the closer range will be average.
2
In the econometric calculations tend to use General, intergroup and intragroup variance. The first describes how the symptom totality under the influence of all factors acting upon it. It can be calculated by the formula:
σ^2общ = (sum(x-khsr)*f)/sum of f, where
khsr – the General arithmetic mean for the whole population.
σ^2общ = (sum(x-khsr)*f)/sum of f, where
khsr – the General arithmetic mean for the whole population.
3
The between-group variance shows how the average deviates each group from the total for all groups. It reflects the influence of the factor is put at the base of the group. It can be found as follows:
σ^2m = (sum(HSR-khsr)*ni)/sum ni, where
HSR is the average value of the characteristic for a particular group;
ni – the number of units in the group;
khsr – average value, characteristic for the total number of groups.
σ^2m = (sum(HSR-khsr)*ni)/sum ni, where
HSR is the average value of the characteristic for a particular group;
ni – the number of units in the group;
khsr – average value, characteristic for the total number of groups.
4
Intra-group (residual) variance characterizes the fluctuation of the characteristic within each group. She talks about random variations and do not depend on the basis, forms the basis of the group. For its calculation, you must first find the variance for individual groups:
σ^2ві = (sum(x-HCR)*ni)/sum ni, where
HSR average for each group.
And then the average for all groups according to the formula:
σ^2іср = (sum(σ^2ві*ni)/sum ni.
σ^2ві = (sum(x-HCR)*ni)/sum ni, where
HSR average for each group.
And then the average for all groups according to the formula:
σ^2іср = (sum(σ^2ві*ni)/sum ni.
5
They are all intertwined: the total variance is equal to the sum of intergroup and intragroup medium. This ratio reflects the rule of addition the dispersions. It can be represented as follows:
σ^2общ = σ^2m+ σ^2іср
σ^2общ = σ^2m+ σ^2іср
6
Using this rule, you can determine what portion of the total variance is influenced by the trait-factor, which underlay the groups. The higher the proportion of between-group variance in General, the stronger the influence of this factor.