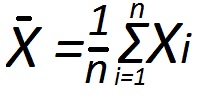You will need
- Knowledge of math.
Instruction
1
Suppose that we are given a set of four numbers. Need to find average value of this set. To do this, first find the sum of all these numbers. Let's say the numbers 1, 3, 8, 7. Their sum is equal to S = 1 + 3 + 8 + 7 = 19. A set of numbers must consist of numbers of the same sign, otherwise the point in calculating the average value is lost.
2
The average value of a set of numbers equal to the sum of the numbers S, divided by the number of these numbers. That is, the average value is equal to 19/4 = 4.75.
3
To set the number also can be found not only higher arithmetic, but also the mean geometric. Several geometric average of positive real numbers is called a number to replace each of these numbers so that their product has not changed. The geometric mean G is searched according to the formula: the nth root of the degree of the product of the set of numbers, where N is the number of numbers in the set. Consider the same set of numbers: 1, 3, 8, 7. Find their average geometric. To do this, calculate the work: 1*3*8*7 = 168. Now from among the 168 you must remove the root of the 4th degree: G = (168)^1/4 = 3.61. Thus the average geometric set of numbers is equal to 3.61.
Note
The average value can not be greater than the largest number in the set and smaller than the small.
Useful advice
In mathematical statistics the mean value is a mathematical expectation.