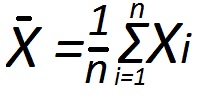How to calculate the probability

The probability of the event means, in essence, share the belief that a certain result will occur or not. Let you have some event And, for example, roll of the dice is an equilateral cube. We need to calculate the probability that it will drop 2 points. In order to calculate the probability P of an event A is found by dividing the number of favorable events n cases of loss 2 points to the total number of events m.

Count the number of cases of loss of 2 points on the dice. This is possible only in one case – when the dice will be 2 points, in any other case, the amount will be more. Thus, the number of favorable events n = 1.

Count the number of cases of loss of any of the numbers on the dice. 1 dice the possible options of hair loss points:
1, 2, 3, 4, 5, 6. Thus, the number of all favourable cases m = 6.

Calculate the probability of loss of 2 points on the dice: P = n/m= 1/6. Thus, only the likelihoodth 1/6 of the dice will be 2 points, the chances are slim.

If there are several auspicious events – for example, it is necessary that bones fell to (less than or equal to 4 points, then you need to add the total number of favorable events n = n1 + n2 + ...+ nx and divide it by the total number of cases. In this case, the cube will be up to 4 points if you get the following points: 1, 2, 3, 4 – all 4 options. Thus, the number of favorable events n = 4. Now the probability of loss up to 4 points on the dice:
P = n/m= 4/6 = 2/3 – already more than half, the risk to lose is the third (if you roll 5 or 6).

In order to correctly calculate the probability, don't forget to count absolutely all possible results, which will be the denominator, and remember that if something is not taken into account, the result will show the big share of probability, which can be a mistake. Upon the occurrence of simultaneous outcomes of several events is sometimes important priority of getting a result, then the total number of events is further increased.