Instruction
1
In order to choose the right formula of reliability, determine the value of groups of samples. If the number of measurements is greater than 30, such a group would be considered large. Thus, there are three options: both groups are small, the two large groups, one small group, the second – biggest.
2
In addition, you will need to know, dependent on whether the measurement of the first group with the second measurement. If each i-th variant of the first group opposed to the i-th embodiment of the second group, they are pairwise dependent. If the options within the group can be interchanged, such groups are called groups with pairwise-independent variants.
3
For comparison of groups with pairwise-independent options (at least one of them must be big), use the formula presented in the figure. Using the formula you can find the student's criterion, it determines a confidence probability of the differences between the two groups.

4
To determine the student's t-test for small size groups with pairwise-independent options, use another formula, it is represented in the second picture. The number of degrees of freedom is calculated in the same way as in the first case: fold the volume of the two samples and subtract the number 2.
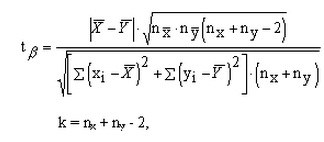
5
To compare two small groups with pairwise-dependent results using two formulas of your choice. The number of degrees of freedom is calculated differently according to the formula k=2*(n-1).
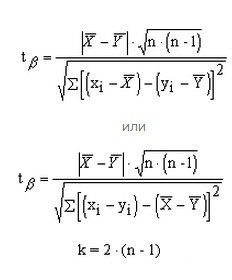
6
Next, specify confidence probability according to the table t-student's t test. In this case, note that the sample was reliable, confidence probability must be at least 95%. That is, find the first column value of the number of degrees of freedom, and the first line is a calculated student's criterion and rate, more or less, the resulting probability of 95%.
7
For example, you received t=2,3; k=73. On the table to determine a confidence probability, it is more than 95%, therefore, the differences of the samples is accurate. Another example: t=1,4; k=70. According to the table below to the minimum value for 95% confidence, k=70, t must be equal to at least of 1.98. You have the same it is less - only 1.4, so the difference of the samples unreliable.
