How to find the height of a trapezoid if you know all sides

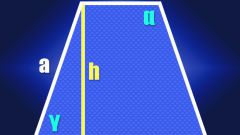
Non-parallel sides of a trapezoid are called lateral sides, and parallel bases. Line between the bases, perpendicular to them - the height of the trapezoid. If the lateral sides of a trapezoid are equal, then it is called isosceles. First, consider the solution of a trapezoidthat is not isosceles.

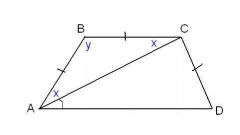
Guide BE cut from point B to lower the base AD parallel to the side of the trapezoid CD. Since BE and CD are parallel and held between the parallel bases of the trapezoid is BC and DA, then BCDE is a parallelogram, its opposite sides BE and CD are equal. BE=CD.

Consider the triangle ABE. Calculate the direction of AE. AE=AD-ED. The base of the trapezoid , BC and AD are known, and in the parallelogram BCDE opposite sides BC and ED are equal. ED=BC, then AE=AD-BC.

Now find out the area of triangle ABE in the formula of Heron, calculating properiter. S=sqrt(p*(p-AB)*(p-BE)*(p-AE)). In this formula, p is properiter triangle ABE. p=1/2*(AB+BE+AE). To compute the area, you are aware of all necessary data: AB, BE=CD, AE=AD-BC.

Next, write down the area of the triangle ABE in another way - it is equal to half of the work of the triangle's height BH and the sides AE, to which it is held. S=1/2*BH*AE.

Express from this formula the height of the triangle that is the height of the trapezoid. BH=2*S/AE. Calculate it.

If isosceles trapezoid, the solution is to do differently. Consider the triangle ABH. It is rectangular, as one of the corners, BHA, direct.

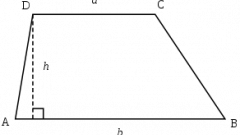
Swipe from the top C height CF.

Examine the figure of the HBCF. HBCF rectangle, since two sides are the height and the other two are the bases of the trapezoid, that is, the straight angles, and opposite sides are parallel. This means that BC=HF.

Look at right triangles ABH and FCD. The angles at the elevation BHA and CFD are straight, and the angles at the lateral sidesx BAH and CDF are equal, since the trapezoid ABCD is isosceles, then the triangles are similar. Because of the height BH and CF are equal or the lateral side of the isosceles trapezoid , AB and CD are equal, then these triangles are equal. Hence, their sides AH and FD is also equal.

Find AH. AH+FD=AD-HF. Because of the parallelogram HF=BC, and triangles, AH=FD, then AH=(AD-BC)*1/2.

Further, from the right triangle ABH Pythagoras to calculate the height BH. The square of the hypotenuse AB is equal to the sum of the squares of the sides AH and BH. BH=sqrt(AB*AB AH*AH).