Instruction
1
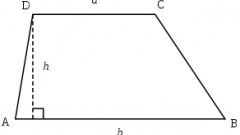
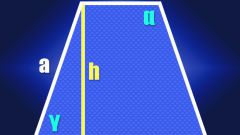
Draw a rectangular trapezoid ABCD. The sides of this figure indicate, respectively, as AB and DC. The first side DC coincides with the height of the trapezoid. It is perpendicular to two rectangular bases of the trapezoid.
There are several ways of finding the sides. So for example, if the task is given to the second lateral side BA and the angle ABH=60, then the height of the first find the most simple of ways, having a height of BH:
BH=AB*sinα
Since BH=CD, then CD=AB*sinα=√3AB/2
2
If, on the contrary, given of the trapezoid is denoted as CD, and you want to find her the same side of AB, this problem is solved in some other way. Since BH=CD and at the same time, BH is a leg of the triangle ABH, we can conclude that the side AB is equal to:
AB=BH/sinα=2BH/√3
3
The problem can be solved and in that case, if the angle is unknown, provided that the two bases and the side AB. However, in this case, you can only find the side CD, which is the height of the trapezoid. Initially, knowing the value of the grounds, find the length of line AH. It is equal to the difference between the larger and the smaller bases, because we know that BH=CD:
AH=AD-BC
Then, using the Pythagorean theorem, find the height BH is equal to the side CD:
BH=√AB^2-AH^2
4
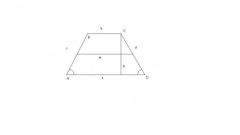
If a rectangular trapezoid has the diagonal BD and angle 2α, as shown in figure 2, the side AB can also be found by the Pythagorean theorem. To do this, first calculate the length of base AD:
AD=BD*cos2α
Then find the side AB in the following way:
AB=√BD^2-AD^2
Then prove the similarity of triangles ABD and BCD. Since these triangles share one common side - diagonal, and thus, two angles are equal, as can be seen from the figure, these shapes are similar. Based on this evidence, find the second lateral side. If you know the upper base and the diagonal, you find the normal way using a standard spherical law of cosines:
c^2=a^2+b^2-2ab cos α, where a, b, C be the sidelengths of a triangle, α is the angle between sides a and b.