How to calculate the height of a trapezoid

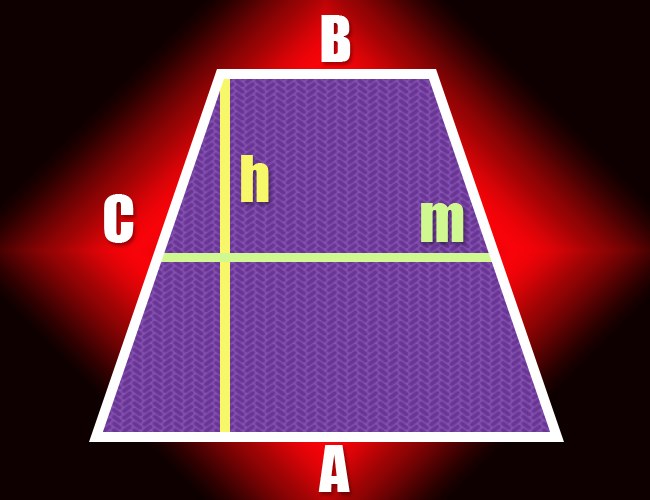
If in terms of the lengths of both bases (a and b) and area (S) of the trapezoid, start calculating the height (h) find the half-sum of the lengths of the parallel sides: (a+b)/2. Then the resulting value divide the area - the result is the required size: h = S/((a+b)/2) = 2*S/(a+b).

Knowing the length of the middle line (m) and area (S), you can simplify the formula from the previous step. By definition the middle line of a trapezoid is equal to the sum of its bases, so to calculate the height (h) of the figure simply divide the area for the length of the midline: h = S/m.

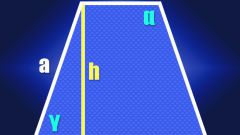
You can determine the height (h) of the quadrilateral, and in that case, if given only the length of one of the sides (C) and the angle (α) formed by her and a long base. In this case, you should consider the triangle formed by this side, a height, and a short segment of the base, which cuts lowered to his height. The triangle is rectangular, known side will be the hypotenuse and the height is the leg. The ratio of the lengths of the leg and of the hypotenuse is equal to the sine of the opposite leg. of the angle, so to calculate the height of a trapezoid multiply the known side length to the sine of the known angle: h = s*sin(α).

The same triangle should be considered and if the length of the sides (C) and the angle (β) between it and the others (short) base. In this case, the angle between the side (the hypotenuse) and height (leg) will be 90° less is known of the conditions of an angle of β-90°. Since the ratio of the lengths of the leg and of the hypotenuse is equal to the cosine of the angle between them, the height of the trapezoid is calculate by multiplying the reduced cosine 90° angle to the length of the sides: h = C*cos(β-90°).

If a trapezoid inscribed in a circle of known radius (r), the calculation formula of height (h) is very simple and does not require knowledge of any other parameters. The circle, by definition, must touch each of the bases by only one point and these points will lie on the same line as the center of the circle. This means that the distance between them is equal to the diameter (twice the radius), held perpendicular to the bases, that is, coinciding with the height of a trapezoid: h=2*r.