How to find the angles of an isosceles trapezoid

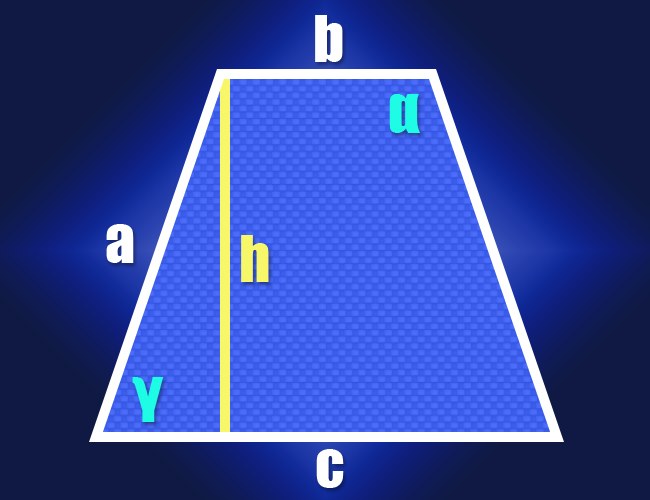
If you know the lengths of both bases (b and c) and the same definition of side (a) of an isosceles trapezoid, to calculate the value of one of its acute angles (γ) we can use the properties of a right triangle. This will lower the height of any adjoining short base angle. A right triangle will be formed with a height (side) side side (the hypotenuse) and cut the long base between the height and the near side (the second side). The length of this segment can be found by taking the length of the long base length of the smaller and dividing the result in half: (c-b)/2.

Having obtained values of the lengths of two adjacent sides of a right triangle, proceed to the calculation of the angle between them. The ratio of the length of the hypotenuse (a) to the length of the leg ((c-b)/2) gives the cosine of this angle (cos(γ)), as a function of the inverse cosine will help convert it into a value of angle in degrees: γ=arccos(2*a/(c-b)). So you will receive the value of one of the acute angles of the trapezoid, and since it is isosceles, then the second acute angle will have the same value. The sum of all the angles of a quadrilateral should be 360°, this means that the sum of two obtuse angles is equal to the difference between this number and the doubled value of the acute angle. As both a blunt angle will also be same, for finding the magnitude of each (α) this difference must be divided in half: α = (360°-2*γ)/2 = 180°-arccos(2*a/(c-b)). Now you have a formula calculate all the angles of an isosceles trapezoid according to the known lengths of its sides.

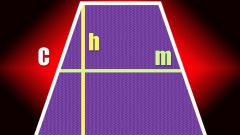
If the lengths of the sides of the figures is unknown, but given its height (h), then we must act according to the same scheme. In this case, in a right triangle, composed of the height, the sides are cut long and short base, you will know the lengths of two sides. Their ratio defines the tangent of the desired angle, and this trigonometric function also has its antipode, which converts the tangent value into the angle value of the arc tangent. Obtained in the previous step formula acute and obtuse angles transform accordingly: γ=arctg(2*h/(c-b)) and α = 180°-arctg(2*h/(c-b)).