Instruction
1
The problem of finding an arbitrary angle in a trapezoid requires enough additional data. Consider an example in which two base angle of a trapezoid. Let the known angles ∠BAD and ∠CDA, we find the angles ∠ABC and ∠BCD. A-line has a property such that the sum of the angles on each side equal to 180°. Then ∠ABC = 180°-∠BAD and ∠BCD = 180°-∠CDA.
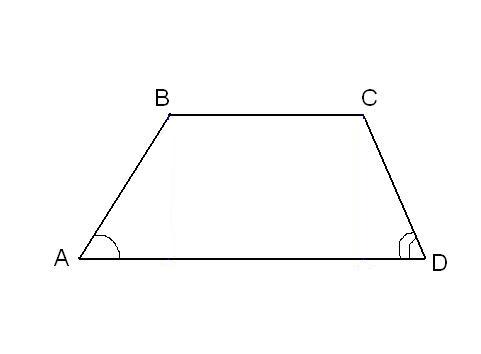
2
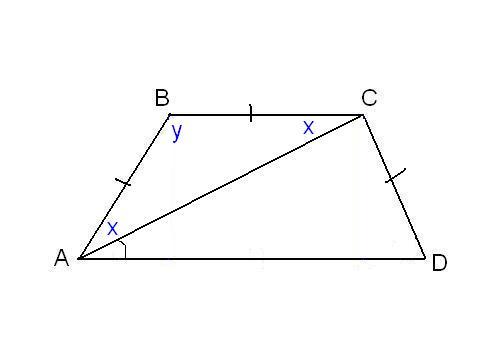
Another problem can be the equal sides of the trapezoid and any additional corners. For example, as shown, may be aware that the sides AB, BC and CD are equal, and the diagonal is from lower base angle ∠CAD = α.Consider the trianglepolygon ABC, it is isosceles as AB = BC. Then ∠BAC = ∠BCA. Let us denote it x for short, and ∠ABC - y. The sum of the angles of any triangle,anglea is 180°, it follows that 2x + y = 180°, then y = 180° - 2x. At the same time of the properties of a trapezoid: y + x + α = 180° and therefore 180° - 2x + x + α = 180°. Thus, x = α. We found two angles of a trapezoid: ∠BAC = 2x = 2α and ∠ABC = y = 180° - 2α.Since AB = CD by hypothesis, then the trapezoid is isosceles or isosceles. So the diagonal are equal and equal angles at the bases. Thus, ∠CDA = 2α and ∠BCD = 180° - 2α.