How to find side of a trapezoid if you know the base

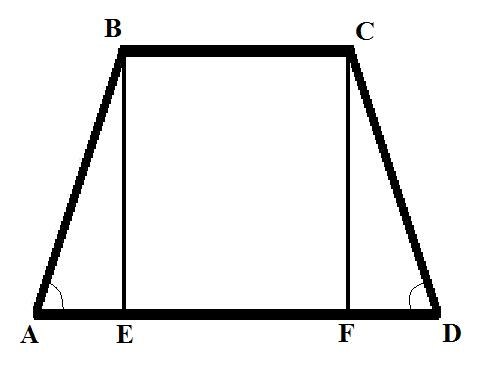
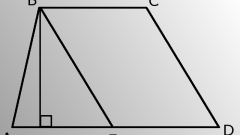
Consider two tasks with different initial data.Task 1.Find the lateral side of the isosceles trapezoidif you know the base BC = b, the base AD = d and the angle at the side of the BAD = alpha.Solution:Drop a perpendicular (the height of the trapezoid) from the vertex B to the intersection with the large basism, will receive a cut BE. Write down the formula for AB using the measure of the angle: AB = AE/cos(BAD) = AE/cos(alpha).

Find the AE. It would be the difference of the lengths of the two bases, divided in half. So: AE = (AD - BC)/2 = (d - b)/2.Now find AB = (d - b)/(2*cos(alpha)).In an isosceles trapezoid the lengths of the sides are equal, hence CD = AB = (d - b)/(2*cos(alpha)).

Task 2.Find the lateral side of the trapezoid AB, if you know the upper base BC = b; lower base AD = d; the height BE = h and the angle opposite the side of the CDA is equal to alpha.Solution:do a second height from vertex C to the intersection with the lower basisof m, will receive a cut of CF. Consider the right triangle CDF, find the direction FD according to the following formula: FD = CD*cos(CDA). The length of the side CD, find another formula: CD = CF/sin(CDA). So: FD = CF*cos(CDA)/sin(CDA). CF = BE = h, therefore, FD = h*cos(alpha)/sin(alpha) = h*ctg(alpha).

Consider the right triangle ABE. Knowing the length of sides AE and be, you can find the third side - the hypotenuse AB. You are aware of the length of the side BE find AE as follows: AE = AD - BC - FD = d - b - h*ctg(alpha).Using the following property of a right triangle - the square of the hypotenuse is equal to the sum of the squares of two - way AB:AB(2) = h(2) + (d - b - h*ctg(alpha))(2).The lateral sides of the trapezoid AB is the square root of the expression on the right side of the equality.