You will need
- To know the area of a trapezoid, the lengths of the bases and also the length of the middle line.
Instruction
1
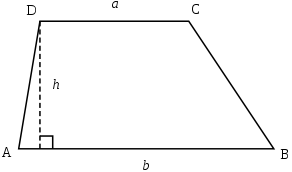
In order to calculate the area of a trapezoid, you must use the following formula:
S = ((a+b)*h)/2, where a and b are the bases of the trapezoid, h is the height of the trapezoid.
In that case, if the area and lengths of bases are known, find the elevation by the formula:
h = (2*S)/(a+b)
S = ((a+b)*h)/2, where a and b are the bases of the trapezoid, h is the height of the trapezoid.
In that case, if the area and lengths of bases are known, find the elevation by the formula:
h = (2*S)/(a+b)
2
If the trapeze is known for its size and length of the middle line, then find its height will not be difficult:
S = m*h where m is the middle line here:
h = S/m.
S = m*h where m is the middle line here:
h = S/m.
3
In order to make both more understandable, you can give a couple of examples.
Example 1: length of the midline of the trapezoid is 10 cm, its area is 100 cm2. To find the height of the trapezoid is necessary to perform the action:
h = 100/10 = 10 cm
Answer: the height of this trapezoid is 10 cm
Example 2: the area of the trapezoid is 100 cm2, the length of the bases equal to 8 cm and 12 cm find the height of the trapezoid need to run the action:
h = (2*100)/(8+12) = 200/20 = 10 cm
Answer: the height of this trapezoid is 20 cm
Example 1: length of the midline of the trapezoid is 10 cm, its area is 100 cm2. To find the height of the trapezoid is necessary to perform the action:
h = 100/10 = 10 cm
Answer: the height of this trapezoid is 10 cm
Example 2: the area of the trapezoid is 100 cm2, the length of the bases equal to 8 cm and 12 cm find the height of the trapezoid need to run the action:
h = (2*100)/(8+12) = 200/20 = 10 cm
Answer: the height of this trapezoid is 20 cm
Note
There are several types of trapezoids:
An isosceles trapezoid is such a trapezoid in which the sides are equal.
Rectangular trapezoid is trapezoid, which has one internal angle equal to 90 degrees.
It should be noted that in a rectangular trapezoid height is equal to the length of a side at a right angle.
Around the trapezoid can be circumscribed by a circle, or enter her in this shape. To enter a circle only if the sum of its bases is equal to the sum of the opposite sides. To describe the circumference is possible only around an isosceles trapezoid.
An isosceles trapezoid is such a trapezoid in which the sides are equal.
Rectangular trapezoid is trapezoid, which has one internal angle equal to 90 degrees.
It should be noted that in a rectangular trapezoid height is equal to the length of a side at a right angle.
Around the trapezoid can be circumscribed by a circle, or enter her in this shape. To enter a circle only if the sum of its bases is equal to the sum of the opposite sides. To describe the circumference is possible only around an isosceles trapezoid.
Useful advice
A parallelogram is a special case of a trapezoid, because the definition of a trapezoid does not contradict the definition of a parallelogram. A parallelogram is a quadrilateral with opposite sides parallel to each other. The trapezoid as in the definition it is only a couple of his parties. So every parallelogram is a trapezoid. The opposite is not true.