Instruction
1
The General formula
Use the General formula of the square to an arbitrary quadrilateral:
S=1/2•AC•BD•sinφ, where AC and BD of the length of the diagonal, φ is the angle between the diagonals.
Use the General formula of the square to an arbitrary quadrilateral:
S=1/2•AC•BD•sinφ, where AC and BD of the length of the diagonal, φ is the angle between the diagonals.
2
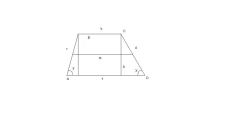
If you want to prove or derive this formula, break up the trapezoid into 4 triangles. Write down the formula for the area of each triangles is (1/2 works sides by the sine of the angle between them). Take the angle which is formed by the intersection of the diagonals. Next, use the property of additivity of area: record the area of the trapezoid as the sum of the areas of its constituent triangles. Group the components, clearing the multiplier 1/2 and the sine of the brackets (given that sin(180°-φ)=sinφ). Get the original formula the area of this rectangle.
In General, it is useful to consider the area of the trapezoid as the sum of the areas of its constituent triangles. Often this is the key to solving the problem.
In General, it is useful to consider the area of the trapezoid as the sum of the areas of its constituent triangles. Often this is the key to solving the problem.
3
Important theorems
Theorem which may be necessary if the numerical value of the angle between the diagonals is not specified explicitly:
1) the Sum of all the angles of a triangle equal 180°.
In General, the sum of all the angles of a convex polygon is equal to 180°•(n-2), where n is the number of sides of the polygon (equal to the number of its corners).
2) the Theorem of sines for a triangle with sides a, b and c:
a/sinA=b/sinB=c/sinC where A, B, C are angles lying opposite the sides a, b, c respectively.
3) the Theorem of cosines for a triangle with sides a, b and c:
c2=a2+b2-2•a•b•cosα, where α is the angle of the triangle formed by sides a and b. The theorem of the cosines of its famous special case of the Pythagorean theorem since cos90°=0.
Theorem which may be necessary if the numerical value of the angle between the diagonals is not specified explicitly:
1) the Sum of all the angles of a triangle equal 180°.
In General, the sum of all the angles of a convex polygon is equal to 180°•(n-2), where n is the number of sides of the polygon (equal to the number of its corners).
2) the Theorem of sines for a triangle with sides a, b and c:
a/sinA=b/sinB=c/sinC where A, B, C are angles lying opposite the sides a, b, c respectively.
3) the Theorem of cosines for a triangle with sides a, b and c:
c2=a2+b2-2•a•b•cosα, where α is the angle of the triangle formed by sides a and b. The theorem of the cosines of its famous special case of the Pythagorean theorem since cos90°=0.
4
The special properties of a trapezoid - rawalakot
Note the properties of the trapezoid specified in the problem statement. If given an isosceles trapezoid (lateral faces are equal), use the property that the diagonals are equal in it.
Note the properties of the trapezoid specified in the problem statement. If given an isosceles trapezoid (lateral faces are equal), use the property that the diagonals are equal in it.
5
The special properties of a trapezoid - the presence of a right angle
If you are given a rectangular trapezium (one of the corners of the trapezoid a straight line), consider the rectangular triangles inside of a trapezoid. Remember that the area of a right triangle is equal to half of the work of its sides forming a right angle, since sin90°=1.
If you are given a rectangular trapezium (one of the corners of the trapezoid a straight line), consider the rectangular triangles inside of a trapezoid. Remember that the area of a right triangle is equal to half of the work of its sides forming a right angle, since sin90°=1.