You will need
- calculator
Instruction
1
Trapezoid is a quadrilateral with two sides parallel to the ground, and the other two not parallel sides. Trapezoid, the sides of which are equal, is called isosceles or ravnovesnoi. If in an isosceles trapezoid the diagonals are perpendicular, then the height is equal to the sum of bases, we consider the case when diagonals are not perpendicular.
2
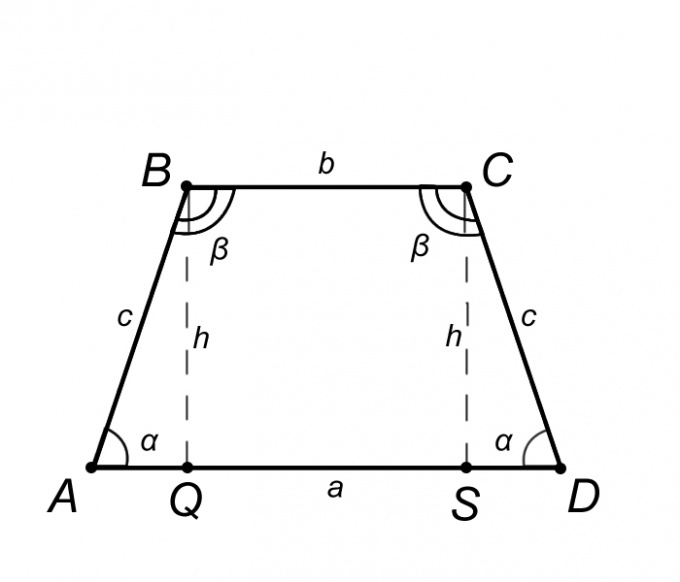
Consider an isosceles trapezoid ABCD and describe its properties, but only those, knowledge of which will help us to solve the problem. From the definition of an isosceles trapezoid, the base AD = a is parallel to BC = b, and side AB = CD = c, it follows that the angles at the bases equal, that is, the angle BAQ = CDS = α, in the same way, the angle ABC = BCD = β. Summing up, it is fair to say that the triangle ABQ is equal to the triangle SCD, and hence, cut off AQ = SD = (AD – BC)/2 = (a – b)/2.
3
If in the problem statement we are given the lengths of the bases a and b and length of side C, the height h of the trapezoid is equal to the segment BQ is as follows. Consider the triangle ABQ, because, by definition, the height of the trapezoid is perpendicular to the base, it can be argued that the triangle ABQ rectangular. Side of the AQ triangle ABQ, based on the properties of an isosceles trapezoid, is given by AQ = (a – b)/2. Now knowing the two sides AQ and c by the Pythagorean theorem, find the height h. The Pythagorean theorem States that the hypotenuse squared is equal to the sum of the squares of the legs. We write this theorem applied to our problem: c^2=AQ^2+ h^2. It follows that h = √(c^2-AQ^2).
4
For example, consider the trapezoid ABCD in which the base AD = a = 10cm BC = b = 4 cm, side AB = c = 12cm. To find the height of a trapezoid h. Find the side of the AQ triangle ABQ. AQ = (a – b)/2 = (10-4)/2=3cm. Then substitute the values of the sides of the triangle in the Pythagorean theorem. h = √(c^2-AQ^2) = √(12^2-3^2) =√135=11.6 see
Useful advice
Properties of an isosceles trapezoid.
A straight line passing through the middle of the bases perpendicular to the bases is the axis of symmetry of the trapezoid.
Height, lowered from the top on the larger base, divides it into two segments, one of which is equal to the sum of the bases, the other half-difference basis.
In an isosceles trapezoid the angles at either base are equal.
In an isosceles trapezoid the length of the diagonals.
About an isosceles trapezoid can be circumscribed by a circle.
If in an isosceles trapezoid the diagonals are perpendicular, then the height is equal to the sum of the bases.
A straight line passing through the middle of the bases perpendicular to the bases is the axis of symmetry of the trapezoid.
Height, lowered from the top on the larger base, divides it into two segments, one of which is equal to the sum of the bases, the other half-difference basis.
In an isosceles trapezoid the angles at either base are equal.
In an isosceles trapezoid the length of the diagonals.
About an isosceles trapezoid can be circumscribed by a circle.
If in an isosceles trapezoid the diagonals are perpendicular, then the height is equal to the sum of the bases.