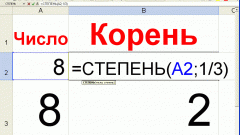
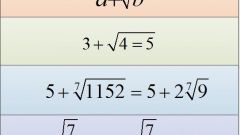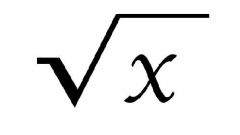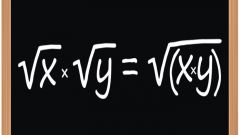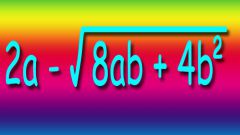How to make a number of root

In most cases, it's easier to calculate on the calculator radical expression. But if you want to solve the problem in General or radical expression contains the unknown variables or the conditions of the problem it is necessary only to simplify, not to calculate, will have to find ways of making any number of under root.

How to make a number of root
How to solve examples with roots
How to extract the square root of fractions
How do I output the number of root

Instruction

Use the definition of rootas a mathematical operation, from which it follows that the extraction of a root is the inverse operation of raising a number to a power. This means that the number can be taken from under the root if the decrease in radical expressions , the number of times that corresponds to a raised to the power passed. For example, to take from under the square root of the number 10, divide remaining under the root expression of ten squared.

Pick up the radical number of this multiplier, making of which is under root do simplify the expression - otherwise the operation will lose meaning. For example, if under the sign of the root with exponent equal to three (cubic root), is the number 128, then out of sign can be taken, for example, the number 5. In this radical , the number 128 will have to be divided by 5 cubed: 3√128 = 5∗3√(128/53) = 5∗3√(128/125) = 5∗3√1.024. If the presence of fractional numbers under the sign of root is not contrary to the conditions of the problem, the solution can be left in this form. If you need a more simple variant, we first divide radical expression for such an integer multiplier, cube root one of which will be a whole numberC. for Example: 3√128 = 3√(64∗2) = 3√(43∗2) = 4∗3√2.

Use for the selection of the multipliers radical number calculator, if you calculate in the mind the powers of a number is not possible. This is especially important for the rootm with the exponent greater than two. If you have Internet access, you can calculate the built-in Google search engine and Nigma solvers. For example, if you need to find the largest integer multiplier, which can be taken from under the sign of the cubic root for numbers 250, then going to Google enter "6^3" to check, can you just take out of sign of root six. The search engine displays the result equal to 216. Alas, the 250 cannot be divided without a remainder is the number. Then enter the query 5^3. The result will be 125, and it allows you to break 250 on the multipliers 125 and 2, and therefore to stand under the sign of the root number 5, leaving the number 2.

Is the advice useful?