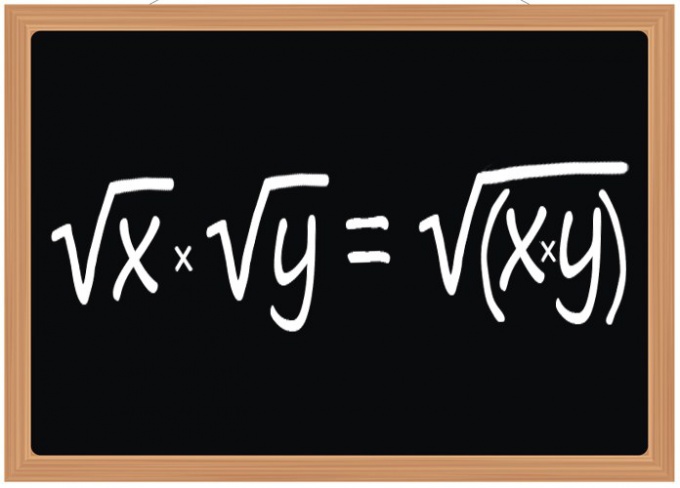How to multiply square root square root

One of the four elementary mathematical operations (multiplication) has created another, somewhat more sophisticated exponentiation. That, in turn, has added additional complexity in the teaching of mathematics, giving rise to reverse a surgery - extraction of root. Any of these operations, you can use any other mathematical operation, which further confuses the study of the subject. To make it all somehow organize, there are sets of rules, one of which reglementary the order of multiplication of the roots.

Instruction

Use for multiplication of square roots rule, the result should be the square root, radicals which is the product of radical expressions roots of multipliers. This rule applies when multiplying two, three or any other number of square roots. However, it applies not only to the roots of the quadratic, but cubic, or any other exponent, if this figure is the same for all involved in the operation of the radicals.

If the signs multiply roots are numerical values, multiply them together and place the resulting value under the root. For example, when multiplying √3,14 on √a 7.62 this action can be written as: √3,14 * √7,62 = √(3,14*7,62) = √23,9268.

If radical expressions contain variables, we first write the product under the same radical sign, and then try to simplify radical expression is obtained. For example, if it is necessary to multiply √(x+7) √(x-14) operation can be written as: √(x+7) * √(x-14) = √((x+7) * (x-14)) = √(x2-14*x+7*x-7*14) = √(x2-7*x-98).

If you need to multiply more than two square roots act in the same way - gather under one radical sign radical expression multiply all the roots as multipliers of one complex expression, and then simplify it. For example, when multiplying square roots of numbers 3,14, 7,62 and 5,56 can be written as: √3,14 * √7,62 * √5,56 = √(3,14*7,62*5,56) = √133,033008. And the multiplication of the square roots derived from expressions with variables x+7, x-14 and 2*x+1, so: √(x+7) * √(x-14) * √(2*x+1) = √((x+7) * (x-14) * (2*x+1)) = √((x2-14*x+7*x-7*14) * (2*x+1)) = √((x2-7*x-98) * (2*x+1)) = √(2*x*x2-2*x*7*x-2*x*98 + x2-7*x-98) = √(2*x3-14*x2-196*x+x2-7*x-98) = √(2*x3-13*x2-205*x-98).

Is the advice useful?