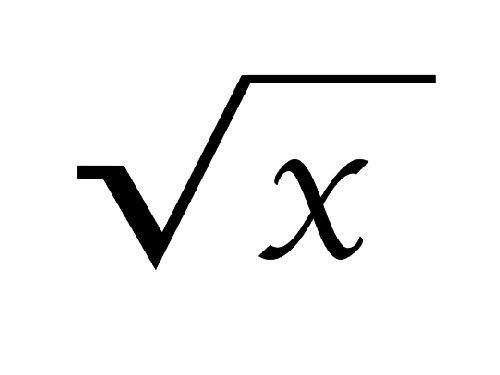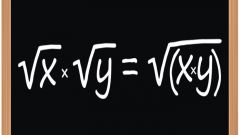Instruction
1
The root of n-th degree of number a is such a number that if you build it in the n-th degree, get a number and. The root may have up to two solutions or have no solutions at all. This definition is valid when the action is performed on a real number, both positive and negative. In the field of complex numbers the root is always the number of decisions that coincide with its degree.
2
Root of real numbers, like other arithmetic operations, has several General properties:
• The square root of zero is also zero 0;
• The root of the unit also the unit 1;
• Root of the product of two numbers or expressions is equal to the product of the roots of these expressions with non-negative values;
• The root of the division of two quantities is equal to the ratio of the roots of these values when the value of the divisor not equal to zero;
• The root of the n-th extent of the number and can be written in the form a^(1/n);
• The root of the n-th extent of the number a raised to the power of m, can be written in the form a^(m/n);
• When taking the root from the root the number and extent of roots are multiplied, i.e. (a^(1/n))^(1/m) = a^(1/mn).
• The root of an odd power of a negative number is a negative number;
• The root of an even degree of a negative number does not exist.
• The square root of zero is also zero 0;
• The root of the unit also the unit 1;
• Root of the product of two numbers or expressions is equal to the product of the roots of these expressions with non-negative values;
• The root of the division of two quantities is equal to the ratio of the roots of these values when the value of the divisor not equal to zero;
• The root of the n-th extent of the number and can be written in the form a^(1/n);
• The root of the n-th extent of the number a raised to the power of m, can be written in the form a^(m/n);
• When taking the root from the root the number and extent of roots are multiplied, i.e. (a^(1/n))^(1/m) = a^(1/mn).
• The root of an odd power of a negative number is a negative number;
• The root of an even degree of a negative number does not exist.
3
When marking is used root sign √. The degree of the root is written above it, the square root (second degree), it is not written. The root is called quadratic if its multiplication by itself gives the number.
4
The roots of the equation are elements of the set of solutions of this equation. The decision is such value of unknown variable in which the equation will make sense.
Note
There is an unofficial Holiday Square root, which is celebrated nine times in a hundred years, in the days when the number and the ordinal number of the month are the square root of the last two digits of the year. For example 02/02/02 or 04/04/16, etc.