You will need
- calculator.
Instruction
1
To calculate root of the third degree, take a calculator designed for engineering calculations. To calculate root of the third degree, use the equivalent function of raising to the power 1/3.
2
To raise a number to the power 1/3, enter that number, then click on exponentiation and enter the approximate value of the number 1/3 - 0,333. Such accuracy is sufficient for most calculations. However, the accuracy of calculation is very easy to improve – just add as many triples, how many will fit on the display of the calculator (for example, 0,3333333333333333). Then click "=".
3
To calculate root of the third degree using the computer, run the Windows calculator. The procedure for calculating root of third degree fully similar to that described above. The only difference is in the design of the buttons exponentiation. On the virtual keyboard of the calculator it is labelled as "x^y".
4
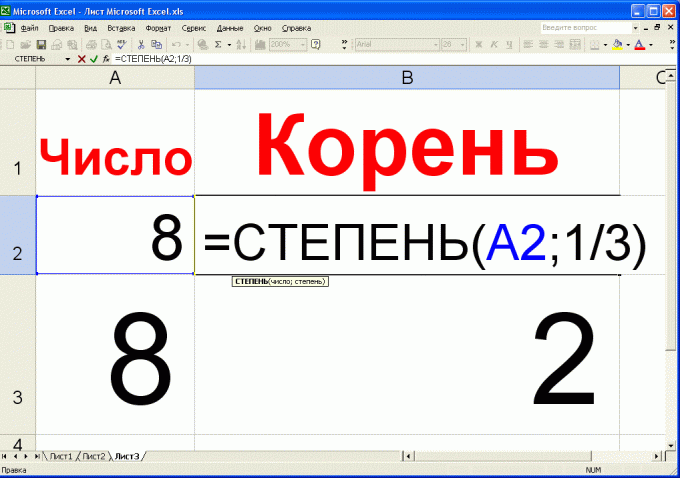
The root of the third degree can be calculated in MS Excel. To do this, enter in any cell of the symbol "=" and select the "insert function" (fx). Select menu option "DEGREE" and click "OK". In appeared window enter the number for which you want to calculate root of the third degree. In the window, "Degree", enter the number "1/3". Dial the number 1/3 exactly in this form – as an ordinary fraction. After that, click "OK". In that cell of the table where the created formula will appear in the cube root of a given number.
5
If the root of the third degree has to calculate constantly, then slightly improve the above-described method. As the number from which you want to extract the root, specify not the number itself, and the cell of the table. After that, each time you enter in that cell of the original number in the cell with the formula will appear its cube root.
Note
Conclusion. In this paper we have discussed various methods of calculating values of the cube root. It turned out that the values of the cube root can be found with the help of the method of iterations, it is also possible to approximate the cube root, raise a number to the power of 1/3 to find the values of the root of the third degree with Microsoft Office Ecxel, setting formulas in cells.
Useful advice
The roots of the second and third degree are used especially often and thus have special names. Square root: In this case the exponent is usually omitted, and the term "root" without indicating the extent often implies the square root. Practical computation of the roots of the algorithm for finding the root of n-th degree. Square roots and cube roots are usually included in all the calculators.