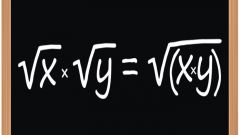How to make a multiplier at the root

The root of a number x is a number that when raised to a degree of a root is equal to x. A multiplier called multiply, the number. That is, in the expression x*ª√y need to make x under the root.

Instruction

Determine the degree of the root. It is usually denoted by a Superscript figure before him. If the degree of the root is not specified, the root is square, its degree is two.

Make the multiplier under the root, elevating him to the degree of the root. That is, x*ª√y = a√(y*xª).

Consider the example 5*√2. The square root, therefore, take the number 5 to a square that is in the second degree. Get √(2*52). Simplify radical expression. √(2*52) = √(2*25) = √50.

Study example 2*3√(7+x). In this case, the root of the third degree, so raise the multiplieroutside of the root, 3 degree. Get 3√((7+x)*23) = 3√((7+x)*8).

Consider the example (2/9)*√(7+x) where you have to make under the root of a fraction. The algorithm of actions is not very different. Erect in the degree of the numerator and denominator of a fraction. Get √((7+x)*(22/92)). Simplify radical expression, if necessary.

Let's do another example, where the multiplier already has a degree. In y2*√(x3) multipliermade under a root, squared. When raised to a new degree and making the root of much just multiplies. That is, after entering under the square root, y2 will be of the fourth degree.

Consider an example in which the degree is a fraction, that is, the multiplier is also under the root. Find it in the example √(y3)*3√(x) degree of x and y. The degree of x is equal to 1/3, that is the root of the third degree, and make under the root of the multiplier y is of degree 3/2, i.e. it is in Cuba and under the square root.

Give the roots to the same extent, to combine radical expressions. To do this, give fractions of degrees to a common denominator. Multiply the numerator and denominator on the same number which will allow you to achieve this.

Find common denominator for fractions degrees. For 1/3 and 3/2 is 6. Multiply both parts of the first fraction by two, and the other three. That is (1*2)/(3*2) and (3*3)/(2*3). It will, accordingly, 2/6 and 9/6. Thus, x and y will be under a common root of the sixth degree, x second, and y in the ninth degree.

Is the advice useful?