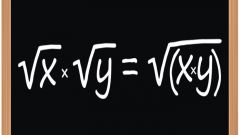How to solve roots

Irrational equations should be rational in order to find the answer, solving it the traditional way. However, in addition to squaring then add one more action: discard the extraneous root. This concept is connected with the irrationality of the roots, i.e. the solution to an equation, substitution of which leads to meaninglessness, for example, the root of a negative number.

Consider a simple example: √(2•x + 1) = 3. Lift both sides of the square:2•x + 1 = 9 → x = 4.

It turns out that x=4 is the root and simultaneously the normal equations 2•x + 1 = 9 and the source of the irrational √(2•x + 1) = 3. Unfortunately, this is not always easy. Sometimes the method of squaring leads to absurdity, for example:√(2•x - 5) = √(4•x - 7)

It would seem, you just need to build both parts in the second degree and all, a solution is found. In reality, however, we get the following:2•x – 5 = 4•x – 7 → -2•x = -2 → x=1.The substitute found the root of the original equation:√(-3) = √(-3).x=1 and is called an extraneous root rational equations that has no other roots.

Now a more complicated example: √(2•x2 + 5•x - 2) = x – 6 ↑22•x2 + 5•x – 2 = x2 – 12•x + 36x2 + 17•x – 38 = 0

Solve ordinary quadratic equation:D = 289 + 152 = 441x1 = (-17 + 21)/2 = 2; x2 = (-17 - 21)/2 = -19.

Substitute x1 and x2 into the original equation to avoid extraneous roots:√(2•22 + 5•2 - 2) = 2 – 6 → √16 = -4;√(2•(-19)2 - 5•19 - 2) = -19 – 6 → √625 = -25.This decision is wrong, therefore, the equation, like the previous one, has no roots.

Example with variable change.Sometimes, the simple construction of both parts of the equation in the square does not release from the roots. In this case, you can use the method of substitution:√(x2 + 1) + √(x2 + 4) = 3 [y2 = x2 + 1]y + √(y2 + 3) = 3 → √(y2 + 3) = 3 – y ^ a 2

y2 + 3 = 9 – 6•and + y26•y = 6 → y=1.x2 + 1 = 1 → x=0.

Check the result:√(02 + 1) + √(02 + 4) = 1 + 2 = 3 – equality are met, then the root x=0 is a valid solution of irrational equations.