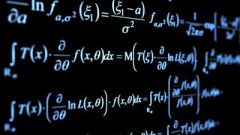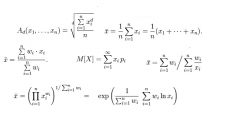How to calculate the probability

The probability of an event is the ratio of the number of all favorable outcomes to the number of all possible outcomes. A favorable outcome is the outcome, which invariably leads to the realization of the event. To understand this better, you need to disassemble a simple example with dice. The probability of rolling a three when throwing dice, is calculated as follows. Just when throwing dice, there are six possible events. They are defined by the number of its faces. But in this case there is only one favorable outcome - a loss of three. Then the probability to throw all three in a single throw of the dice is equal to 1/6. It should be noted that the probability of any event is in the interval from zero to one.

If the desired event can be easily decomposed into several events that are incompatible with each other, then the probability of this desired event is equal to the sum of the probabilities of each of the incompatible events. In mathematical statistics, this statement is called the theorem of addition of probabilities. It can also be considered when throwing dice. Now you need to determine the probability of loss of the odd numbers. Such numbers on the three dice, namely 1, 3 and 5. The probability of each of them is 1/6. By theorem find the probability of loss of the odd numbers. It is equal to the sum of the probabilities of each of these events: 3/6 = 1/2.

Sometimes, you need to determine the probability of occurrence of two independent from each other events. Events Can be considered as independent if their probability of non-occurrence or occurrence does not depend from each other. In this case, the probability of find as the product of the probabilities of occurrence of both events. To understand it better, you need to try to find the probability of hair loss at the same time two sixes on two dice. These events are independent from each other. The probability that on the dice roll of a six is 1/6. So the probability of occurrence of two sixes is 1/36.