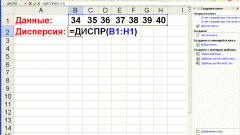
Instruction
1
Any random variable has a number of numerical characteristics that determine its probability and the degree of deviation from the true value. This is the initial and Central moments of different order. The first initial moment is called the mathematical expectationm and the Central moment of second order – dispersion.
2
Mathematical expectation of a random variable is its average expected value. Also this feature is called the center of the probability distribution and find by integration the formula of the Lebesgue-stiltjes:m = ∫xdf(x), where f(x) is a distribution function whose value is the probability of elements of set x ∈ X.
3
Based on the initial definition of the integral of a function, mathematical expectation can be represented as the integral sum of a numeric series, whose members consist of pairs of elements of sets of values of a random variable and its probabilities at these points. Pairs are linked by multiplication: m = Σxi•pi, the interval is the summation of i from 1 to ∞.
4
This formula is a consequence of the Lebesgue integral-stiltjes for the case when the analyzed variable X is discrete. If it is an integer, then calculate the mathematical expectation can be through generating function of the sequence, which is equal to the first derivative of the probability distribution functions at x=1:m = f’(x) = Σk•p_k with 1 ≤ k < ∞.
5
The variance of the random variable used to estimate the average value of squared deviations from the mathematical expectation, or rather of its spread around the center of the distribution. Thus, these two quantities are related by the formula:d = (x - m)2 .
6
Substituting in it the already known representation of the expectation in the integral sum, we can calculate the variance as follows:d = Σpi•(xi - m)2.