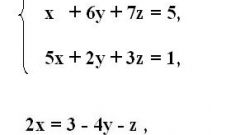Instruction
1
Let's say you have the equation:
2x+y=10
x-y=2
It can be solved in several ways.
2
Way to postuniversity one variable and substitute it into another equation. It is possible to Express any variable of your choice. For example, Express "from the second equation:
x-y=2 => y=x-2Затем all the substitute in the first equation:
2+(x-2)=10Перенесите all the numbers without "x to the right side and calculate:
2x+x=10+2
3=12 Then, to find x , divide both sides of equation by 3:
x=4.So, you have found "x . Find ". To do this, substitute the "x in the equation from where you have expressed ":
y=x-2=4-2=2
y=2.
3
Make the check. To do this, substitute the resulting values into the equations:
2*4+2=10
4-2=2
Unknown found right!
4
Method of addition or subtraction uraninites from some variable. In our case it is easier to do with ".
As in the first equation "the sign", and the second " - then you can perform the operation of addition, i.e. the left part of the fold on the left and the right on the right:
2x+y+(x-y)=10+2Преобразуйте:
2x+y+x-y=10+2
3=12
x=4Подставьте "x in any equation and find ":
2*4+y=10
8+y=10
at=10-8
y=2 on the 1st way you can check that the roots are found true.
5
If there is no clearly defined variables, it is necessary to convert the equation.
In the first equation have a "2 , and the second just "x . To the addition or subtraction of "x was reduced, multiply the second equation by 2:
x-y=2
2-2U=4Затем subtract the first equation from the second:
2x+y-(2x-2Y)=10-4Заметим, if before the parenthesis is minus, then after the disclosure adjust the marks to the opposite:
2x+y-2x+2Y=6
3y=6
y=2"x, find the expressing of any equation, i.e.,
x=4