Instruction
1
Method of addition.
You need to write two equations strictly under each other:
2 –5Y=61
-9x+5Y=-40.
Next, fold each term of the equations, respectively, considering their signs:
2+(-9x)=-7x, -5U+5U=0, 61+(-40)=21. As a rule, one of the sums containing the unknown amount, will be zero.
Write the equation of the resulting members:
-7x+0=21.
The unknown: -7x=21, h=21:(-7)=-3.
Already substitute the value found in any of the original equations and obtain a second unknown, solving a linear equation:
2x–5Y=61, 2(-3)–5Y=61, -6-5Y=61, -5Y=61+6, -5Y=67, y=-13,4.
The response of the system of equations: x=-3, y=-13,4.
You need to write two equations strictly under each other:
2 –5Y=61
-9x+5Y=-40.
Next, fold each term of the equations, respectively, considering their signs:
2+(-9x)=-7x, -5U+5U=0, 61+(-40)=21. As a rule, one of the sums containing the unknown amount, will be zero.
Write the equation of the resulting members:
-7x+0=21.
The unknown: -7x=21, h=21:(-7)=-3.
Already substitute the value found in any of the original equations and obtain a second unknown, solving a linear equation:
2x–5Y=61, 2(-3)–5Y=61, -6-5Y=61, -5Y=61+6, -5Y=67, y=-13,4.
The response of the system of equations: x=-3, y=-13,4.
2
The method of substitution.
One equation should Express any of the required members:
x–5Y=61
-9x+4U=-7.
x=61+5Y, x=61+5U.
Substitute the resulting equation into the second instead of the number "x" (in this case):
-9(61+5Y)+4U=-7.
Then deciding
the linear equation to find the number of "y":
-549+45у+4U=-7, 45у+4U=549-7, 49у=542, y=542:49,≈11.
In randomly selected (from the system) to insert the equation is already found "y" the number 11 and to compute the second unknown:
X=61+5*11 x=61+55, x=116.
Answer the given system of equations: x=116, y=11.
One equation should Express any of the required members:
x–5Y=61
-9x+4U=-7.
x=61+5Y, x=61+5U.
Substitute the resulting equation into the second instead of the number "x" (in this case):
-9(61+5Y)+4U=-7.
Then deciding
the linear equation to find the number of "y":
-549+45у+4U=-7, 45у+4U=549-7, 49у=542, y=542:49,≈11.
In randomly selected (from the system) to insert the equation is already found "y" the number 11 and to compute the second unknown:
X=61+5*11 x=61+55, x=116.
Answer the given system of equations: x=116, y=11.
3
A graphical way.
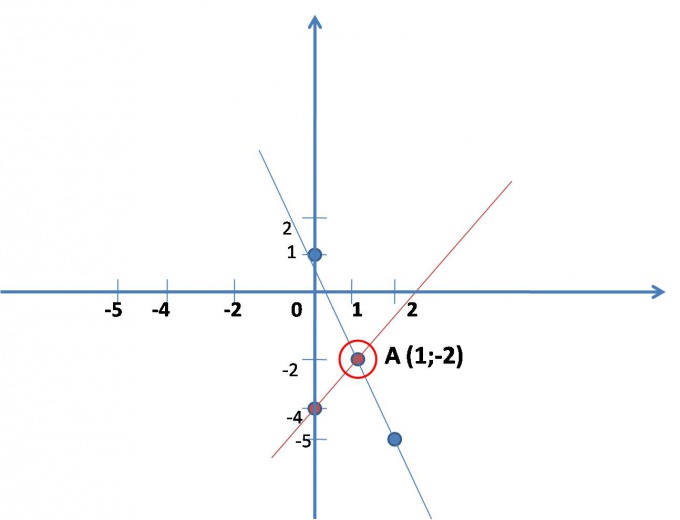
Is to practice finding the coordinates of a point which intersect the lines mathematically written in the system of equations. You should draw graphs of both direct separately in the same coordinate system. The General form of straight line equation: – y=KX+b. To build direct, it is sufficient to find the coordinates of the two points, and x is chosen arbitrarily.
Given the system: 2x – y=4
y=-3x+1.
Video is based on the first equation, for convenience, it should be written: y=2x-4. To invent (easier) the values for x, substituting into equation, solving it, find y. You get two points, which is based on video. (see pic.)
x 0 1
at -4 -2
Video is based on the second equation: y=-3x+1.
To build a direct. (see pic.)
x 0 2
1 to 5
Find the coordinates of the intersection point of two constructed lines on the chart (if the lines do not intersect, then the system of equations has no solution – it happens).
Is to practice finding the coordinates of a point which intersect the lines mathematically written in the system of equations. You should draw graphs of both direct separately in the same coordinate system. The General form of straight line equation: – y=KX+b. To build direct, it is sufficient to find the coordinates of the two points, and x is chosen arbitrarily.
Given the system: 2x – y=4
y=-3x+1.
Video is based on the first equation, for convenience, it should be written: y=2x-4. To invent (easier) the values for x, substituting into equation, solving it, find y. You get two points, which is based on video. (see pic.)
x 0 1
at -4 -2
Video is based on the second equation: y=-3x+1.
To build a direct. (see pic.)
x 0 2
1 to 5
Find the coordinates of the intersection point of two constructed lines on the chart (if the lines do not intersect, then the system of equations has no solution – it happens).
Useful advice
If the same system of equations solved in three different ways, the answer would be the same (if the solution is correct).