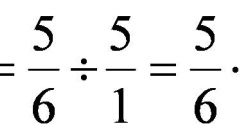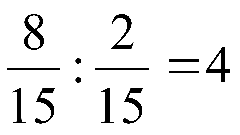Instruction
1
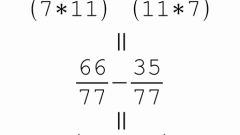
Consider addition and subtraction of fractions. For example, 5/2+10/5. Bring both fractions to a common denominator. To do this, find the number that can be divided without remainder by the denominator of the first and second fractions. In our case this number is 10. Convert the above fraction, obtained 25/10+20/10.
Now add together the numerators, and leave the denominator unchanged. It turns out 45/10.
It is possible to reduce the resulting fraction, i.e., divide the numerator and the denominator by the same number. It turns out 9/2.
Highlight the whole part. Find the maximum number that can be divided without remainder by the denominator. The number 8. Divide it by the denominator - this will be a part of it. So, the result is 4 1/2.
Perform the same steps in subtracting fractions.
Now add together the numerators, and leave the denominator unchanged. It turns out 45/10.
It is possible to reduce the resulting fraction, i.e., divide the numerator and the denominator by the same number. It turns out 9/2.
Highlight the whole part. Find the maximum number that can be divided without remainder by the denominator. The number 8. Divide it by the denominator - this will be a part of it. So, the result is 4 1/2.
Perform the same steps in subtracting fractions.
2
Consider the multiplication of fractions. Here everything is simple. Multiply together the numerators and denominators. For example, 2/5 is multiplied by 4/2 turns 8/10. Simplify the fraction, it turns 4/5.
3
Consider dividing fractions. In this step, you flip one of the fractions, then multiply numerators and denominators. For example, 2/5 divided by 4/2 - turns 2/5 times 2/4 - it turns out 4/20. Simplify the fraction, it turns out 1/5.