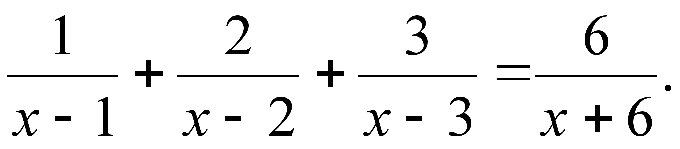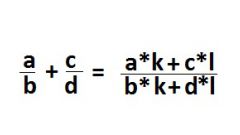Instruction
1
Perhaps the most obvious point here is, of course, the denominator. Numerical fractions do not represent any danger (fractional equations where all denominators are only numbers, will generally be linear), but if the denominator is a variable, then it must be considered and administered. First, it means that the value of x, converting 0 in the denominator, the root can not be, and generally need to separately register the fact that x can't equal this number. Even if you have that if you substitute in the numerator of all perfectly convergent and satisfies the conditions. Second, we can't multiply or divide both sides of the expression equal to zero.
2
After that, the solution of this equation is reduced to the transfer of all of its members in the left part to the right remains 0.
You need to bring all members to a common denominator, domnain, where necessary, the missing numerator of the expression.
Then solve the normal equation, written in the numerator. Can make General the multipliers of the brackets, apply the formulas of reduced multiplication to cause a similar to calculate roots of a quadratic equation using the discriminant, etc.
You need to bring all members to a common denominator, domnain, where necessary, the missing numerator of the expression.
Then solve the normal equation, written in the numerator. Can make General the multipliers of the brackets, apply the formulas of reduced multiplication to cause a similar to calculate roots of a quadratic equation using the discriminant, etc.
3
The result should be factorization into a product of parentheses (x-(i-th root)). This also includes polynomials with no roots, e.g. square trinomial with a discriminant that is less than zero (unless, of course, the problem is to find only real roots, as often happens).
Definitely need to factorize the denominator to find there brackets already present in the numerator. If the denominator of expressions like (x-(number)), it is best when bringing to a common denominator standing there brackets to multiply "in a forehead", and to leave the product source of simple expressions.
The same brackets in the numerator and denominator can be reduced by writing in advance, as mentioned above, the conditions.
The answer is written in brackets how many values of x, or simply by enumeration: x1=..., x2=..., etc.
Definitely need to factorize the denominator to find there brackets already present in the numerator. If the denominator of expressions like (x-(number)), it is best when bringing to a common denominator standing there brackets to multiply "in a forehead", and to leave the product source of simple expressions.
The same brackets in the numerator and denominator can be reduced by writing in advance, as mentioned above, the conditions.
The answer is written in brackets how many values of x, or simply by enumeration: x1=..., x2=..., etc.