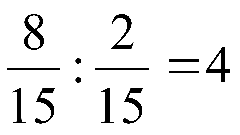You will need
- a textbook on mathematics for 5 and 6 classes
Instruction
1
It is customary to divide common and decimal fractions, familiarity with which begins in high school. Currently there is no area of knowledge where you would not apply this concept. Even in history we're talking the first quarter of the 17th century, and all at once understand what we mean 1600-1625. Also often have to deal with basic operations on fractions and convert from one form to another.

2
Reduction of fractions to a common denominator is perhaps the most important operation on ordinary fractions. This is the basis for all calculations. So, let's say there are two fractions a/b and c/d. Then, in order to bring them to a common denominator, you need to find the least common multiple (M) numbers b and d, and then multiply the numerator of the first fraction to (M/b) and the numerator of the second to (M/d).
3
Compare fractions, is another important task. In order to do this, give a set of simple fractions to a common denominator and then compare numerators whose numerator is greater than the fraction and more.

4
In order to perform the addition or subtraction of ordinary fractions, you need to bring them to a common denominator, and then produce the desired mathematical operation with the numerators of these fractions. The denominator remains unchanged. Let's say you need from a/b subtract c/d. This requires to find the least common multiple of M numbers b and d, and after you subtract one numerator from the other, without changing the denominator: (a*(M/b)-(c*(M/d))/M
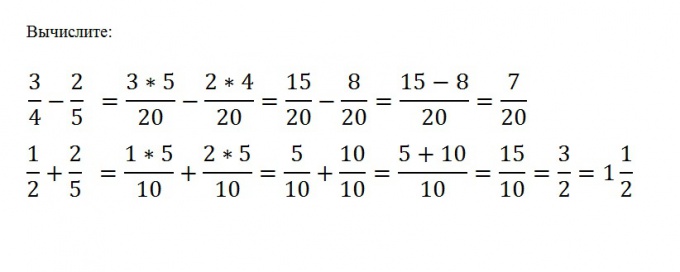
5
Simply multiply one fraction by another, simply multiply their numerators and denominators:
(a/b)*(c/d)=(a*c)/(b*d)to divide one fraction by another, you need a fraction of the dividend multiplied by a fraction the inverse of the divisor. (a/b)/(c/d)=(a*d)/(b*c)
To cost to remind that in order to get the reverse shot, you need the numerator and denominator are reversed.
(a/b)*(c/d)=(a*c)/(b*d)to divide one fraction by another, you need a fraction of the dividend multiplied by a fraction the inverse of the divisor. (a/b)/(c/d)=(a*d)/(b*c)
To cost to remind that in order to get the reverse shot, you need the numerator and denominator are reversed.
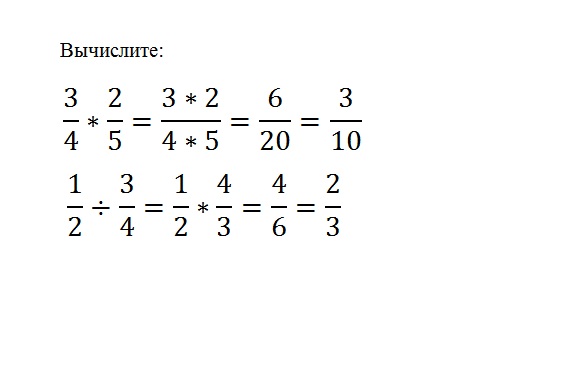
6
Order from the ordinary of the fraction go to a decimal, you need to divide the numerator by the denominator. The result can be both finite and infinite.If the decimal fractions you need to go to an ordinary, lay your number for a whole hour and the fractional presenting the past in the form of a natural number divided by ten to the appropriate degree.

Useful advice
Do not forget to reduce the fraction.