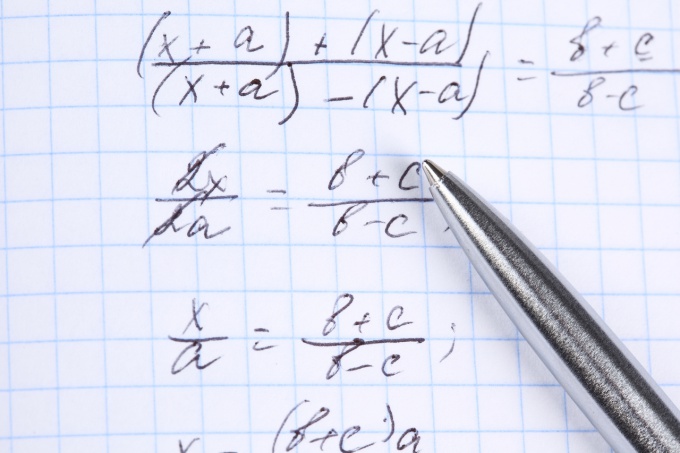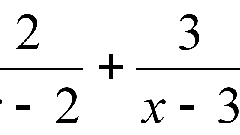Instruction
1
Imagine a fractional inequality so that one side stood a rational expression, and on the other side of the sign - 0. Now the inequality in General form is: f(x)/g(x) > (<, ≤ or ≥) 0.
2
Determine the points at which g(x) changes sign, write down all intervals on which g(x) of constant sign.
3
For each interval, imagine the original fractional expression as a product of functions f(x) and g(x), changing the sign of the inequalitywhen necessary. Actually you multiply left and right part of the inequality on the same number. Thus the sign of inequality is reversed if the number (in our case g(x)) is negative and stays the same if the number is positive. Also while maintaining rigor (>, <) and porous (≤, ≥) inequality.
4
For the resulting inequality f(x)*g(x) > (<, ≤ or ≥) 0 use standard solution methods, but now for each previously detected interval of the number line. One of them will be the same method intervals znakpatenta applied to the function f(x).